题目内容
D、E、F分别为△ABC的边BC、CA、AB上的中点，且
=
，
=
，给出下列命题：
①
=-
-
；
②
=-
+
；
③
=
+
；
④
+
+
=
，
其中正确命题的序号为
| CB |
| a |
| CA |
| b |
①
| AD |
| 1 |
| 2 |
| a |
| b |
②
| BE |
| a |
| 1 |
| 2 |
| b |
③
| CF |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
④
| AD |
| BE |
| CF |
| 0 |
其中正确命题的序号为
②③④
②③④
．分析：如图，由三角形法则依次用两个基向量
=
，
=
，表示出
，
，
，验证知②③④正确．
| CB |
| a |
| CA |
| b |
| AD |
| BE |
| CF |
解答：
解：①
=
+
=-
+
=
-
，故①不正确；
②
=
+
=-
+
=-
+
，故②正确；
③
=
+
=
+
，故③正确；
④将三个向量
，
，
的结果代入知
+
+
=
成立．故④正确．
故②③④正确
故答案为 ②③④．
解：①| AD |
| AC |
| CD |
| CA |
| 1 |
| 2 |
| CB |
| 1 |
| 2 |
| a |
| b |
②
| BE |
| BC |
| CE |
| CB |
| 1 |
| 2 |
| CA |
| a |
| 1 |
| 2 |
| b |
③
| CF |
| 1 |
| 2 |
| CA |
| 1 |
| 2 |
| CB |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
④将三个向量
| AD |
| BE |
| CF |
| AD |
| BE |
| CF |
| 0 |
故②③④正确
故答案为 ②③④．
点评：本题考查向量的加法法则，属于向量三角形法则与平行四边形法则的应用．
练习册系列答案
高效智能课时作业系列答案
相关题目
如图，P-ABC是底面边长为1的正三棱锥，D、E、F分别为棱长PA、PB、PC上的点，截面DEF∥底面ABC，且棱台DEF-ABC与棱锥P-ABC的棱长和相等．（棱长和是指多面体中所有棱的长度之和）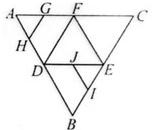
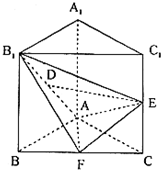（2005•东城区一模）已知直三棱柱ABC-A1B1C1中，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA1=a，D、E、F分别为B1A、C1C、BC的中点．
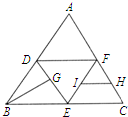如图，在正三角形ABC中，D，E，F分别为AB，BC，AC的中点，G，H，I分别为DE，FC，EF的中点，将