题目内容
设向量a=(x+1,y),b=(x-1,y),点P(x,y)为动点,已知|a|+|b|=4.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P的轨迹与x轴负半轴交于点A,过点F(1,0)的直线交点P的轨迹于B、C两点,试推断△ABC的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由.
答案:
解析:
解析:
|
解:(Ⅰ)由已知, 所以动点P的轨迹M是以点 因为 故动点P的轨迹M的方程是 (Ⅱ)设直线BC的方程为 由 设点 所以 由题设,点A的坐标是(-2,0),则点A到直线BC的距离 所以 令 设 所以当 故△ABC的面积存在最大值,其最大值为 |

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
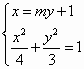
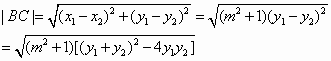
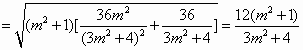 .(8分)
.(8分)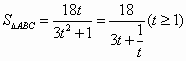 .(10分)
.(10分)