题目内容
设向量a=(x,2),b=(x+n,2x-1)(n∈N+),函数y=a·b在[0,1]上的最小值与最大值的和为an,又数列{bn}满足:nb1+(n-1)b2+…+2bn-1+bn=![]() .
.
(1)求证:an=n+1;
(2)求bn的表达式;
(3)cn=-an·bn,试问数列{cn}中,是否存在正整数k,使得对于任意的正整数n,都有cn≤ck成立?证明你的结论.
答案:
解析:
解析:
|
(1)证明: 所以在[0,1]上为增函数, (2)解:由 得 两式相减得 当 当n≥2时, 即 (3)解:由(1)与(2)得 设存在正整数 当 当 所以当 当 当 所以存在正整数 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
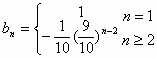 8分
8分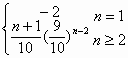 9分
9分