题目内容
已知当椭圆的长轴、短轴、焦距依次成等比时称椭圆为“黄金椭圆”，请用类比的性质定义“黄金双曲线”，并求“黄金双曲线”的离心率为（ ）
A． | B． | C． | D． |
D
解析试题分析：即2a,2b,2c成等比数列。所以
，
，所以
且e>1,
解得e=，关系D。
考点：本题主要考查双曲线的几何性质。
点评：简单题，在圆锥曲线问题中，a,b,c,e的关系，是常考点，它们的内再联系要牢记。
练习册系列答案
相关题目
设
是椭圆
上的一点，
为焦点，且
，则
的面积为（ ）
A． | B． | C． | D．16 |
已知
, 
是椭圆的两个焦点，若满足
的点M总在椭圆的内部，则椭圆离心率的取值范围是（ ）
| A．（0, 1) | B． | C． | D． |
已知抛物线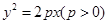
的焦点为
，点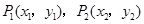
，
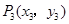在抛物线上，且
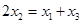， 则有 （ ）
A． | B． |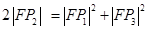
C． | D． |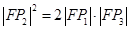
要使直线
与焦点在
轴上的椭圆
总有公共点，实数
的取值范围是（ ）
A． | B． | C． | D． |
双曲线
的一条渐近线的倾斜角为
，离心率为
，则
的最小值为（ ）
A． | B． | C． | D． |
双曲线
的离心率为
，则它的渐近线方程为
A． | B． | C． | D． |
过双曲线的右焦点F作实轴所在直线的垂线，交双曲线于A，B两点，设双曲线的左顶点M，若点M在以AB为直径的圆的内部，则此双曲线的离心率e的取值范围为( )
A．( ，+∞) | B．(1，) | C．(2，+∞) | D．(1，2) |
已知已知点（2，3）在双曲线C：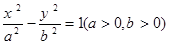
上，C的焦距为4，
则它的离心率为（ ）
| A．2 | B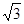． | C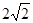． | D． |