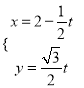题目内容
【题目】已知双曲线C和椭圆![]() 有公共的焦点,且离心率为
有公共的焦点,且离心率为![]() .
.
(1)求双曲线C的方程.
(2)经过点M(2,1)作直线l交双曲线C于A,B两点,且M为AB的中点,求直线l的方程并求弦长.
【答案】(1)x2![]() 1 (2)y=4x﹣7,弦长
1 (2)y=4x﹣7,弦长![]()
【解析】
(1)求出双曲线的焦点坐标,结合离心率,联立求解a,b,c得到双曲线的方程;
(2)设A(x1,y1),B(x2,y2)代入椭圆方程,用点差法求出直线斜率,弦长公式求弦长即可.
(1)由题意得椭圆![]() 的焦点为F1(
的焦点为F1(![]() ,0),F2(
,0),F2(![]() ,0),
,0),
设双曲线方程为![]() 1,a>0,b>0,
1,a>0,b>0,
则c2=a2+b2=3,
∵e![]()
∴c![]() a,
a,
解得a2=1,b2=2,
∴双曲线方程为x2![]() 1.
1.
(2)把A(x1,y1),B(x2,y2)分别代入双曲线x12![]() y12=1,x22
y12=1,x22![]() y22=1,
y22=1,
两式相减,得(x1﹣x2)(x1+x2)![]() (y1﹣y2)(y1+y2)=0,
(y1﹣y2)(y1+y2)=0,
把x1+x2=4,y1+y2=2代入,得4(x1﹣x2)﹣(y1﹣y2)=0,
∴kAB![]() 4,
4,
∴直线L的方程为y=4x﹣7,
把y=4x﹣7代入x2![]() 1,
1,
消去y得14x2﹣56x+51=0,
∴x1+x2=4,x1x2=![]() ,k=4,
,k=4,
∴|AB|![]()
![]() .
.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目