题目内容
若三棱锥的三条侧棱两两相互垂直,且三条侧棱长分别为1,2,3,则其外接球的表面积为分析:由已知中三棱锥的三条侧棱两两相互垂直,且三条侧棱长分别为1,2,3,,故可将其补充为一个长方体,根据外接球的直径等于长方体的对角线,我们求出球的半径,代入球的表面积公式,即可求出答案.
解答:解:∵三棱锥的三条侧棱两两相互垂直,且三条侧棱长分别为1,2,3,,
故可将其补充为一个长宽高分别为1、2、3的长方体,
则其外接球的直径2R=
=
故球的表面积S=4πR2=14π
故答案为:14π.
故可将其补充为一个长宽高分别为1、2、3的长方体,
则其外接球的直径2R=
| 1+4+9 |
| 14 |
故球的表面积S=4πR2=14π
故答案为:14π.
点评:本题考查的知识点是球的体积,其中利用割补法,补充四面体成正方体,进而求出其外接球的半径是解答本题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
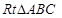 中,若
中,若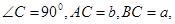 则
则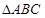 的外接圆半径
的外接圆半径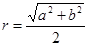 运用类比方法,若三棱锥的三条侧棱两两互相垂直且长度分别为a,b,c,则其外接球的半径R=
.
运用类比方法,若三棱锥的三条侧棱两两互相垂直且长度分别为a,b,c,则其外接球的半径R=
.