题目内容
若三棱锥的三条侧棱两两垂直,且侧棱长均为| 3 |
分析:由于三棱锥的三条侧棱两两垂直,且侧棱长均为
,
将三棱锥扩展为正方体,它的对角线是球的直径,求解即可.
| 3 |
将三棱锥扩展为正方体,它的对角线是球的直径,求解即可.
解答:解:依题可以构造一个正方体,其体对角线就是外接球的直径.2r=
=3,
r=
;
S表面积=4πr2=9π
故答案为:9π.
| 3+3+3 |
r=
| 3 |
| 2 |
S表面积=4πr2=9π
故答案为:9π.
点评:本题考查:立几中的构造法及球的表面积计算;
对于有关外接球的问题要注意归纳几种的典型的构造方法,
再比如正四面体的外接球的构造法,还有对棱相等的构造方法等.
体对角线是外接球的直径,往往有的学生就当成半径来算导致错误.
对于有关外接球的问题要注意归纳几种的典型的构造方法,
再比如正四面体的外接球的构造法,还有对棱相等的构造方法等.
体对角线是外接球的直径,往往有的学生就当成半径来算导致错误.

练习册系列答案
相关题目
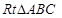 中,若
中,若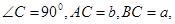 则
则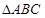 的外接圆半径
的外接圆半径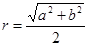 运用类比方法,若三棱锥的三条侧棱两两互相垂直且长度分别为a,b,c,则其外接球的半径R=
.
运用类比方法,若三棱锥的三条侧棱两两互相垂直且长度分别为a,b,c,则其外接球的半径R=
.