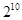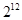题目内容
观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
…
照此规律,第n个等式为________.
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
…
照此规律,第n个等式为________.
n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2
∵1=12,2+3+4=9=32,
3+4+5+6+7=25=52,
4+5+6+7+8+9+10=49=72,
所以第n个等式为
n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2.
3+4+5+6+7=25=52,
4+5+6+7+8+9+10=49=72,
所以第n个等式为
n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2.

练习册系列答案
相关题目
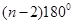 .
. ”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径r=
”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径r= ”;
”; ”类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径r=
”类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径r= ”.这两位同学类比得出的结论( )
”.这两位同学类比得出的结论( ) =c+d
=c+d 排在数表的第n行,第m列,则第m列中的前n个数的和
排在数表的第n行,第m列,则第m列中的前n个数的和 =___________。
=___________。