题目内容
9.已知区域M:$\left\{\begin{array}{l}0≤x≤2\\ 0≤y≤2\end{array}$,定点A(3,1),在M内任取一点P,使得PA≥$\sqrt{2}$的概率为$\frac{5}{4}-\frac{π}{8}$.分析 由题意,画出区域M,和满足PA≥$\sqrt{2}$的部分,利用几何概型公式解答.
解答 解:如图区域M是边长为2的正方形,在M内任取一点P,使得PA≥$\sqrt{2}$的区域是图中阴影部分,面积为4-($\frac{1}{4}π×2-\frac{1}{2}×\sqrt{2}×\sqrt{2}$)=5-$\frac{π}{2}$,
由几何概型公式可得在M内任取一点P,使得PA≥$\sqrt{2}$的概率为$\frac{5-\frac{π}{2}}{2×2}=\frac{5}{4}-\frac{π}{8}$;
故答案为: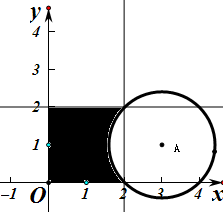 $\frac{5}{4}-\frac{π}{8}$.
$\frac{5}{4}-\frac{π}{8}$.
点评 本题考查了几何概型公式的运用,关键是求出使得PA≥$\sqrt{2}$的部分面积,利用几何概型公式求之.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
17. 如图所示的五个区域中,中心区域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
如图所示的五个区域中,中心区域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
 如图所示的五个区域中,中心区域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
如图所示的五个区域中,中心区域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )| A. | 84 | B. | 72 | C. | 64 | D. | 56 |
4.某单位安排甲、乙、丙三人在某月1日至12日值班,每人4天.
甲说:我在1日和3日都有值班;
乙说:我在8日和9日都有值班;
丙说:我们三人各自值班的日期之和相等.据此可判断丙必定值班的日期是( )
甲说:我在1日和3日都有值班;
乙说:我在8日和9日都有值班;
丙说:我们三人各自值班的日期之和相等.据此可判断丙必定值班的日期是( )
| A. | 2日和5日 | B. | 5日和6日 | C. | 6日和11日 | D. | 2日和11日 |
14.某三棱锥的正视图和俯视图如图所示,则其左视图面积为( )


| A. | 6 | B. | $\frac{9}{2}$ | C. | 3 | D. | $\frac{3}{2}$ |
19.已知φ(x)=x(x-m)2在x=1处取得极小值,且函数f(x),g(x)满足f(5)=2,f′(5)=3m,g(5)=4,g′(5)=m,则函数F(x)=$\frac{f(x)+2}{g(x)}$的图象在x=5处的切线方程为( )
| A. | 3x-2y-13=0 | B. | 3x-2y-13=0或x-2y-3=0 | ||
| C. | x-2y-3=0 | D. | x-2y-3=0或2x+3y-13=0 |