题目内容
定义:对于定义域为D的函数f(x),如果存在t∈D,使得f(t+1)=f(t)+f(1)成立,称函数f(x)在D上是“T”函数.已知下列函数:①f(x)=
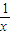 ;
; ②f(x)=log2(x2+2);
③f(x)=2x(x∈(0,+∞));
④f(x)=cosπx(x∈[0,1]),其中属于“T”函数的序号是 .(写出所有满足要求的函数的序号)
【答案】分析:①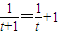 ,属于t2+t+1=0,方程无实数解;
,属于t2+t+1=0,方程无实数解;
②log2[(t+1)2+2]=log2(t2+2)+log23,∴2t2-2t+3=0,方程无实数解;
③2t+1=2t+2,属于t=1>0,即存在t=1∈(0,+∞),使得f(t+1)=f(t)+f(1)成立;
④cos(π+tπ)=costπ-1,所以t= ,此时t+1=
,此时t+1= ∉[0,1].
∉[0,1].
解答:解:①由题意,若存在t∈D,使得f(t+1)=f(t)+f(1)成立,则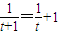 ,整理得t2+t+1=0,方程无实数解,故①不是“T”函数;
,整理得t2+t+1=0,方程无实数解,故①不是“T”函数;
②由定义可得:log2[(t+1)2+2]=log2(t2+2)+log23,即2t2-2t+3=0,方程无实数解,故②不是“T”函数;
③由定义可得:2t+1=2t+2,∴t=1>0,即存在t=1∈(0,+∞),使得f(t+1)=f(t)+f(1)成立,故③是“T”函数;
④由定义可得:cos(π+tπ)=costπ-1,即2costπ=1,解得t= ,此时t+1=
,此时t+1= ∉[0,1],故④不是“T”函数.
∉[0,1],故④不是“T”函数.
综上知,属于“T”函数的序号是③
故答案为:③
点评:本题考查新定义,考查学生的阅读能力,考查学生分析解决问题的能力,属于中档题.
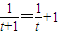 ,属于t2+t+1=0,方程无实数解;
,属于t2+t+1=0,方程无实数解;②log2[(t+1)2+2]=log2(t2+2)+log23,∴2t2-2t+3=0,方程无实数解;
③2t+1=2t+2,属于t=1>0,即存在t=1∈(0,+∞),使得f(t+1)=f(t)+f(1)成立;
④cos(π+tπ)=costπ-1,所以t=
 ,此时t+1=
,此时t+1= ∉[0,1].
∉[0,1].解答:解:①由题意,若存在t∈D,使得f(t+1)=f(t)+f(1)成立,则
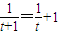 ,整理得t2+t+1=0,方程无实数解,故①不是“T”函数;
,整理得t2+t+1=0,方程无实数解,故①不是“T”函数;②由定义可得:log2[(t+1)2+2]=log2(t2+2)+log23,即2t2-2t+3=0,方程无实数解,故②不是“T”函数;
③由定义可得:2t+1=2t+2,∴t=1>0,即存在t=1∈(0,+∞),使得f(t+1)=f(t)+f(1)成立,故③是“T”函数;
④由定义可得:cos(π+tπ)=costπ-1,即2costπ=1,解得t=
 ,此时t+1=
,此时t+1= ∉[0,1],故④不是“T”函数.
∉[0,1],故④不是“T”函数.综上知,属于“T”函数的序号是③
故答案为:③
点评:本题考查新定义,考查学生的阅读能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 ;
;