题目内容
(2008•深圳一模)设数列{an}的前n项和为Sn,其中an≠0,a1为常数,且-a1、Sn、an+1成等差数列.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=1-Sn,问:是否存在a1,使数列{bn}为等比数列?若存在,求出a1的值;若不存在,请说明理由.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=1-Sn,问:是否存在a1,使数列{bn}为等比数列?若存在,求出a1的值;若不存在,请说明理由.
分析:(Ⅰ)先根据-a1、Sn、an+1成等差数列得到2Sn=an+1-a1;再结合前n项和与通项之间的关系整理即可得an+1=3an(n≥2);得到数列{an}是首项为a1、公比为3的等比数列即可求出{an}的通项公式;
(Ⅱ)先求出数列{bn}的通项公式;结合其通项公式即可求出对应的a1的值.
(Ⅱ)先求出数列{bn}的通项公式;结合其通项公式即可求出对应的a1的值.
解答:解:(Ⅰ)依题意,得2Sn=an+1-a1.于是,当n≥2时,有
.
两式相减,得an+1=3an(n≥2).
又因为a2=2S1+a1=3a1,an≠0,所以数列{an}是首项为a1、公比为3的等比数列.
因此,an=a1•3n-1(n∈N*);
(Ⅱ)因为Sn=
=
a1•3n-
a1,
所以bn=1-Sn=1+
a1-
a1•3n.
要使{bn}为等比数列,当且仅当1+
a1=0,即a1=-2.
|
两式相减,得an+1=3an(n≥2).
又因为a2=2S1+a1=3a1,an≠0,所以数列{an}是首项为a1、公比为3的等比数列.
因此,an=a1•3n-1(n∈N*);
(Ⅱ)因为Sn=
| a1(1-3n) |
| 1-3 |
| 1 |
| 2 |
| 1 |
| 2 |
所以bn=1-Sn=1+
| 1 |
| 2 |
| 1 |
| 2 |
要使{bn}为等比数列,当且仅当1+
| 1 |
| 2 |
点评:本题主要考查等差数列和等比数列的综合问题.其中第一问涉及到了已知前n项和如何求通项问题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
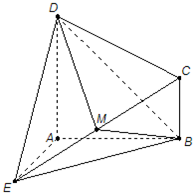 (2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.
(2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.