题目内容
 如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E、F分别是SC和AB的中点,则EF=
如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E、F分别是SC和AB的中点,则EF=| 2 |
| 2 |
分析:先取BC的中点D,连接ED与FD,根据中位线定理可知ED∥SB,FD∥AC,根据题意可知三角形EDF为等腰直角三角形,然后解三角形即可.
解答: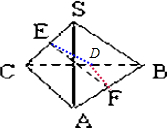 解:取BC的中点D,连接ED与FD
解:取BC的中点D,连接ED与FD
∵E、F分别是SC和AB的中点,点D为BC的中点
∴ED∥SB,FD∥AC
而SB⊥AC,SB=AC=2则三角形EDF为等腰直角三角形
则ED=FD=1,即EF=
故答案为:
.
 解:取BC的中点D,连接ED与FD
解:取BC的中点D,连接ED与FD∵E、F分别是SC和AB的中点,点D为BC的中点
∴ED∥SB,FD∥AC
而SB⊥AC,SB=AC=2则三角形EDF为等腰直角三角形
则ED=FD=1,即EF=
| 2 |
故答案为:
| 2 |
点评:本题主要考查了中位线定理,以及异面直线所成角的应用,同时考查了转化与划归的思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
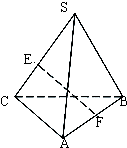 如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E、F分别是SC和AB的中点,则EF的长是( )
如图所示,点S在平面ABC外,SB⊥AC,SB=AC=2,E、F分别是SC和AB的中点,则EF的长是( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|


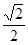 D.
D.

 C.
C. D.
D.
