Question

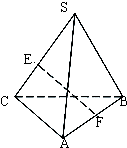如图所示，点S在平面ABC外，SB⊥AC，SB=AC=2，E、F分别是SC和AB的中点，则EF的长是（　　）

• A、1
• B、

  2

• C、

  2

  2

• D、

  1

  2

Answer 1

分析：先取BC的中点D，连接ED与FD，根据中位线定理可知ED∥SB，FD∥AC，根据题意可知三角形EDF为等腰直角三角形，然后解三角形即可．

解答：解：取BC的中点D，连接ED与FD
∵E、F分别是SC和AB的中点，点D为BC的中点
∴ED∥SB，FD∥AC
而SB⊥AC，SB=AC=2则三角形EDF为等腰直角三角形
则ED=FD=1即EF=

2

故选：B

点评：本题主要考查了中位线定理，以及异面直线所成角的应用，同时考查了转化与划归的思想，属于基础题．