题目内容
过点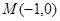 的直线
的直线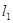 与抛物线
与抛物线 交于
交于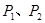 两点,记线段
两点,记线段 的中点为
的中点为 ,过点
,过点 和这个抛物线的焦点
和这个抛物线的焦点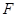 的直线为
的直线为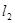 ,
,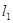 的斜率为
的斜率为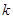 ,则直线
,则直线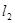 的斜率与直线
的斜率与直线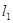 的斜率之比可表示为
的斜率之比可表示为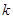 的函数
的函数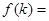 __ .
__ .
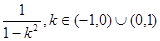
解析试题分析:抛物线 的焦点为F(1,0)依题意,直线
的焦点为F(1,0)依题意,直线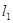 的方程为y=k(x+1),代入
的方程为y=k(x+1),代入 整理得,
整理得, ,由韦达定理可得,P点横坐标为
,由韦达定理可得,P点横坐标为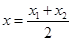 =
=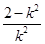 ,纵坐标为
,纵坐标为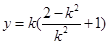 ,所以,直线
,所以,直线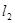 的斜率为
的斜率为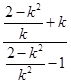 ,直线
,直线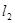 的斜率与直线
的斜率与直线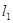 的斜率之比可表示为
的斜率之比可表示为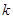 的函数
的函数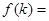
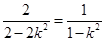 ,
,
故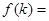
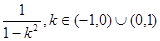
考点:直线与抛物线的位置关系
点评:中档题,涉及直线与抛物线的位置关系问题,往往联立方程组,应用韦达定理,简化解题过程。

练习册系列答案
相关题目
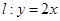 上一点
上一点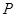 作圆
作圆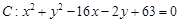 的切线
的切线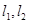 ,若
,若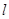 对称,则点
对称,则点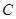 的距离为 .
的距离为 .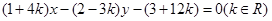 所经过的定点
所经过的定点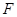 恰好是椭圆
恰好是椭圆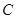 的一个焦点,且椭圆
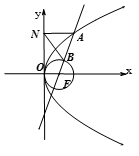
的一个焦点,且椭圆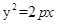 (p>0)的焦点为F,A为C上的点,以F为圆心,
(p>0)的焦点为F,A为C上的点,以F为圆心, 为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠
为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠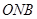 = .
= .
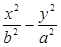 =1的两条渐近线互相垂直,那么该双曲线的离心率是 .
=1的两条渐近线互相垂直,那么该双曲线的离心率是 .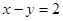 与抛物线
与抛物线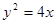 交于
交于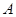 、
、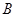 两点,则线段
两点,则线段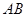 的中点坐标是 。
的中点坐标是 。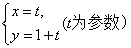 与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为
与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为  是过抛物线
是过抛物线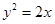 焦点的弦,
焦点的弦,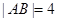 ,则
,则 的一个焦点
的一个焦点 的直线与椭圆交于
的直线与椭圆交于 、
、 两点,则
两点,则 构成
构成 ,那么
,那么