题目内容
在等差数列是{an}中,已知a4与a2与a8的等比中项,a3+2是a2与a6的等差中项,Sn是前n项和,则满足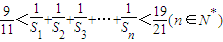 的所有n值的和为 .
的所有n值的和为 .
【答案】分析:由a4是a2与a8的等比中项,a3+2是a2与a6的等差中项,可求得公差、首项,进而得到通项an,从而求得Sn及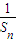 ,于是可求出
,于是可求出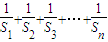 ,解不等式
,解不等式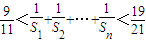 ,由n的范围可确定n值,其和易求.
,由n的范围可确定n值,其和易求.
解答:解:设等差数列是{an}的公差为d,由a4是a2与a8的等比中项,得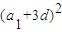 =(a1+d)(a1+7d),化简得
=(a1+d)(a1+7d),化简得 ①,
①,
由a3+2是a2与a6的等差中项,得2(a1+2d+2)=(a1+d)+(a1+5d),解得d=2,代入①得a1=d=2.
所以an=a1+(n-1)•d=2n,
则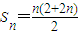 =n(n+1),
=n(n+1),
所以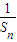 =
=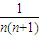 =
=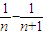 ,
,
则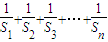 =1-
=1- +
+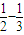 +
+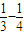 +…+
+…+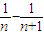 =1-
=1-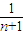 ,
,
由已知得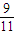 <1-
<1-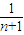 <
<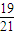 ,解得
,解得 <n<
<n<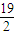 ,
,
又n∈Z,所以n=5,6,7,8,9,且5+6+7+8+9=35,
故答案为:35.
点评:本题考查等差数列与等比数列的综合、数列求和问题,属中档题,通项公式、求和公式及相关基本方法是解决问题的基础.
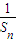 ,于是可求出
,于是可求出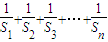 ,解不等式
,解不等式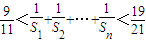 ,由n的范围可确定n值,其和易求.
,由n的范围可确定n值,其和易求.解答:解:设等差数列是{an}的公差为d,由a4是a2与a8的等比中项,得
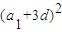 =(a1+d)(a1+7d),化简得
=(a1+d)(a1+7d),化简得 ①,
①,由a3+2是a2与a6的等差中项,得2(a1+2d+2)=(a1+d)+(a1+5d),解得d=2,代入①得a1=d=2.
所以an=a1+(n-1)•d=2n,
则
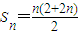 =n(n+1),
=n(n+1),所以
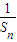 =
=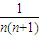 =
=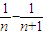 ,
,则
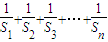 =1-
=1- +
+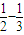 +
+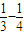 +…+
+…+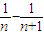 =1-
=1-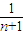 ,
,由已知得
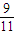 <1-
<1-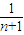 <
<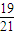 ,解得
,解得 <n<
<n<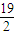 ,
,又n∈Z,所以n=5,6,7,8,9,且5+6+7+8+9=35,
故答案为:35.
点评:本题考查等差数列与等比数列的综合、数列求和问题,属中档题,通项公式、求和公式及相关基本方法是解决问题的基础.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
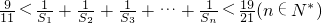 的所有n值的和为________.
的所有n值的和为________.