Question

（本小题满分12分）

已知函数f(x)=log _a 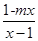(a>0且a≠1)的图像关于原点对称

（1）求m的值；  

（2）判断函数f(x)在区间（1，+∞）上的单调性并加以证明；

（3）当a>1，x∈(t,a)时, f(x)的值域是（1，+∞），求a与t的值。

 

 

Answer 1

【答案】

解：（1）由已知f(-x)=-f(x) 即l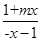og_a+log_a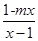=0         ………………………….1分

∴（1-mx）(1+mx)=(x+1)(1-x)      1-m²x²=1-x²                 ∴m=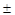1    …………….3分

当m=1时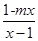，=-1＜0 舍去     ∴ m=-1                                ……………….4分

（2）由（1）得f(x)=log_a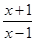 任取1＜x₁＜x₂

f(x₂)- f(x₁)= log_a- log_a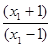= log_a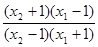   

∵1＜x₁＜x₂  ∴(x₂+1)(x₁-1)-(x₂-1)(x₁+1)=2(x₁-x₂) ∴0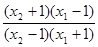＜＜1

当a∈（0,1）时 log_a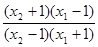＞0，∴f(x₂) ＞ f(x₁),此时f(x)为增函数…7

当a∈（1，+∞）时 log_a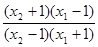＜0，∴f(x₂) ＜ f(x₁) 此时为减函数。.8分            

（3）有（2）知：当a＞1时，f(x)在（1，+∞）为减函数

由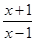＞0有x＜-1或x＞1∴(t,a) 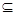（1，+∞）        …………………………..9分

即f(x)在(t,a)上递减，∴f(a)=1, ∴a=1+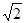，且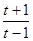→+∞，∴t=1 ……………12分

 

【解析】略