题目内容
已知数列{an},其前n项和为Sn.
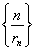
(1)若对任意的n∈N,a2n-1,a2n+1,a2n组成公差为4的等差数列,且a1=1, =2013,求n的值;
=2013,求n的值;
(2)若数列 是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+
是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+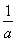 .
.
(1)n=1005(2)见解析
【解析】(1)【解析】
因为a2n-1,a2n+1,a2n组成公差为4的等差数列,
所以a2n+1-a2n-1=4,a2n=a2n-1+8(n∈N*),
所以a1,a3,a5,…,a2n-1,a2n+1是公差为4的等差数列,且a2+a4+a6+…+a2n=a1+a3+…+a2n-1+8n.
又因为a1=1,所以S2n=2(a1+a3+…+a2n-1)+8n=2 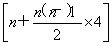 +8n=4n2+6n=2n(2n+3),
+8n=4n2+6n=2n(2n+3),
所以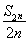 =2n+3=2013,所以n=1005.
=2n+3=2013,所以n=1005.
(2)证明:因为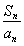 +a=(a+1)qn-1,所以Sn=(a+1)qn-1an-aan,①
+a=(a+1)qn-1,所以Sn=(a+1)qn-1an-aan,①
所以Sn+1=(a+1)qnan+1-aan+1,②
②-①,得(a+1)(1-qn)an+1=[a-(a+1)qn-1]an.③
(ⅰ)充分性:因为q=1+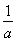 ,所以a≠0,q≠1,a+1≠aq,代入③式,得
,所以a≠0,q≠1,a+1≠aq,代入③式,得
q(1-qn)an+1=(1-qn)an.因为q≠-1,q≠1,
所以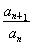 =
=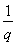 ,n∈N*,所以{an}为等比数列,
,n∈N*,所以{an}为等比数列,
(ⅱ)必要性:设{an}的公比为q0,则由③得
(a+1)(1-qn)q0=a-(a+1)qn-1,
整理得(a+1)q0-a=(a+1) 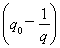 qn,
qn,
此式为关于n的恒等式,若q=1,则左边=0,右边=-1,矛盾;
若q≠±1,当且仅当 时成立,所以q=1+
时成立,所以q=1+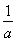 .
.
由(ⅰ)、(ⅱ)可知,数列{an}为等比数列的充要条件为q=1+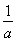 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目