题目内容

下列结论正确的是
 
．
①不等式x2≥4的解集为{x|x≥±2}
②不等式x2-9＜0的解集为{x|x＜3}
③不等式（x-1）2＜2的解集为{x|1-
2
＜x＜1+
2
}
④设x1，x2为ax2+bx+c=0的两个实根，且x1＜x2，则不等式ax2+bx+c＜0的解集为{x|x1＜x＜x2}
分析：①不等式的解法为：（x-2）（x+2）≥0即x≥2或x≤-2；②不等式解法为：（x+3）（x-3）＜0即-3＜x＜3；③解法为：
（x-1+
2
）（x-1-
2
）＜0即1-
2
＜x＜1+
2
；④设x1，x2为ax2+bx+c=0的两个实根，且x1＜x2，则不等式ax2+bx+c＜0的解集应考虑a的正负才能得到解集．
解答：解：分别解出四个不等式的解集得：
①不等式的解法为：（x-2）（x+2）≥0即x≥2或x≤-2；
②不等式解法为：（x+3）（x-3）＜0即-3＜x＜3；
③解法为：（x-1+
2
）（x-1-
2
）＜0即1-
2
＜x＜1+
2
；
④设x1，x2为ax2+bx+c=0的两个实根，且x1＜x2，则不等式ax2+bx+c＜0的解集：当a＞0时，x∈（x1，x2）；当a＜0时，x＞x2或x＜x1．
所以结论正确的是③
故答案为③
点评：考查学生解一元二次不等式的能力．
练习册系列答案
相关题目
设函数f（x）=ax+bx-cx，其中c＞a＞0，c＞b＞0．若a，b，c是△ABC的三条边长，则下列结论正确的是
①②③
①②③
．（写出所有正确结论的序号）
①?x∈（-∞，1），f（x）＞0；
②?x∈R，使ax，bx，cx不能构成一个三角形的三条边长；
③若△ABC为钝角三角形，则?x∈（1，2），使f（x）=0．
对于非零向量
m
，
n
，定义运算“*”：
m
*
n
=|
m
|•|
n
|sinθ其中θ为
m
，
n
的夹角，有两两不共线的三个向量
a
、
b
、
c
，下列结论正确的是（　　）
对于函数y=2sin(2x+
π
6
)，则下列结论正确的是（　　）
（2012•芜湖二模）定义在R上的偶函数f （x）满足f （2-x）=f（x），且在[-3，-2]上是减函数，α，β是钝角三角形的两个锐角，则下列结论正确的是（　　）
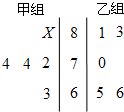精英家教网如图所示茎叶图记录了甲乙两组各5名同学的数学成绩．甲组成绩中有一个数据模糊，无法确认，在图中以X表示．若两个小组的平均成绩相同，则下列结论正确的是（　　）
A、X=2，S甲2＜S乙2B、X=2，S甲2＞S乙2C、X=6，S甲2＜S乙2D、X=6，2，S甲2＞S乙2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网