题目内容
设椭圆的方程为(Ⅰ)用θ、m、n表示四边形ABCD的面积S;
(Ⅱ)若m、n为定值,当θ在(0,![]() ]上变化时,求S的最小值u;
]上变化时,求S的最小值u;
(Ⅲ)如果μ>mn,求![]() 的取值范围.
的取值范围.
答案:
解析:
解析:
解:(Ⅰ)设经过原点且倾角为θ的直线方程为y=xtanθ,可得方程组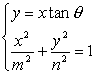 又由对称性,得四边形ABCD为矩形,同时0<θ< 又由对称性,得四边形ABCD为矩形,同时0<θ<(Ⅱ)S= (1)当m>n,即 由于0<θ≤ 故tanθ= (2)当m<n,即 由于
因为0<tanθ1<tanθ2≤1,m2tanθ1tanθ2-n2<m2-n2<0,所以(m2tanθ2+ 所以u= (Ⅲ)(1)当 (2)当 所以 得 综上,当u>mn时, |

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 .
.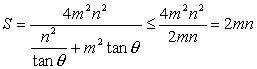 .
.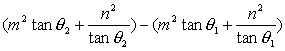
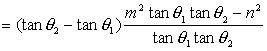 .
.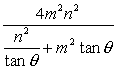 是θ的增函数,故取θ=
是θ的增函数,故取θ=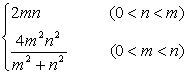
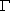 的方程为
的方程为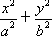 =1(a>b>0),A(0,b)、B(0,-b)和Q(a,0)为
=1(a>b>0),A(0,b)、B(0,-b)和Q(a,0)为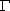 的三个顶点.
的三个顶点. 于C、D两点,交直线l2∶y=k2x于点E.若k1·k2=
于C、D两点,交直线l2∶y=k2x于点E.若k1·k2= ,证明:E为CD的中点;
,证明:E为CD的中点;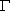 内且不在x轴上,如何构作过PQ中点F的直线l,使得l与椭圆
内且不在x轴上,如何构作过PQ中点F的直线l,使得l与椭圆 的两个交点P1,P2满足
的两个交点P1,P2满足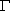 上的点P1,P2满足
上的点P1,P2满足