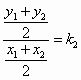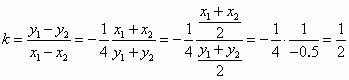Question

已知椭圆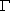的方程为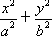＝1(a＞b＞0)，A(0，b)、B(0，－b)和Q(a，0)为的三个顶点．

(1)若点M满足，求点M的坐标；

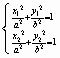
(2)设直线l₁∶y＝k₁x＋p交椭圆于C、D两点，交直线l₂∶y＝k₂x于点E．若k₁·k₂＝，证明：E为CD的中点；

(3)设点P在椭圆内且不在x轴上，如何构作过PQ中点F的直线l，使得l与椭圆的两个交点P₁，P₂满足？令a＝10，b＝5，点P的坐标是(－8，－1)．若椭圆上的点P₁，P₂满足，求点P₁，P₂的坐标．

Answer 1

答案：
解析：

(1)解：． 　　(2)证：设，则由 　　 　　可得，又，故可得 　　而由题意知，所以，即 　　即线段的中点在直线上，也即直线与的交点为线段的中点． 　　(3)椭圆方程为，从而线段的中点为Q(1，－0.5)， 　　若，则为平行四边形，从而线段与线段互相平分，故直线的斜率存在，可设为，直线为y＝k(x－1)－0.5． 　　设，则由 　　可得 　　可得 　　所以直线方程为．