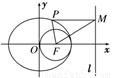
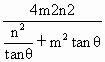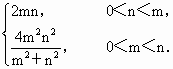题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解析:设经过原点且倾角为 |
(2) |
S= ①当m>n,即 由于0< ②当m<n,即 因为0<tan 是 所以u= |
(3) |
①当 ②当 又由 综上,当u>mn时, 点评:本题主要考查椭圆的对称性及不等式的应用,通过求最大值来考查逻辑思维能力和应用能力,同时体现分类讨论思想. |

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
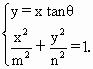 又由对称性,得四边形ABCD为矩形,同时0<
又由对称性,得四边形ABCD为矩形,同时0<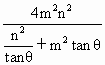 .
. ≤
≤