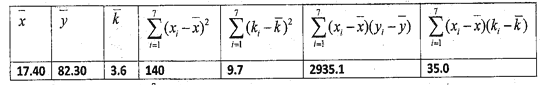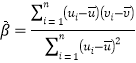题目内容
【题目】如图,在正三棱柱![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的动点,且
上的动点,且![]() .
.
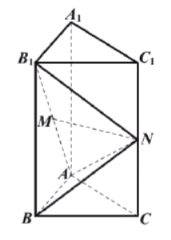
(1)若![]() ,求证:
,求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)若直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,求
,求![]() 的最大值
的最大值
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)取![]() 中点
中点![]() ,通过线线垂直证明
,通过线线垂直证明![]() 平面
平面![]() ,从而得到
,从而得到![]()
(2)取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() 即为二面角
即为二面角![]() 的平面角,再利用余弦定理求出其余弦值.
的平面角,再利用余弦定理求出其余弦值.
(3)利用等体积法,求出![]() 到平面
到平面![]() 的距离及
的距离及![]() 的长度,从而表示出
的长度,从而表示出![]() 关于
关于![]() 的函数,求出最大值.
的函数,求出最大值.
(1)取![]() 中点
中点![]() ,联结
,联结![]() 和
和![]() ,
,
∵![]() ,
,![]() 为
为![]() 中点,又
中点,又![]() 为
为![]() 中点,
中点,![]() ,
,
![]() ,
,![]() ,
,
同理![]() ,
,![]() 平面
平面![]() ,
,![]() ;
;
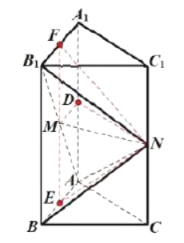
(2)取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连接
,连接![]() ,
,
则![]() ,
,![]() ,
,![]() 即为二面角
即为二面角![]() 的平面角,
的平面角,
设![]() ,则
,则![]() ,
,
![]() ,即二面角
,即二面角![]() 的余弦值为
的余弦值为![]()
(3)设![]() ,
,![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
则![]() ,
,![]()
由等体积法,![]() ,即
,即![]() ,
,
可得![]() ,
,
而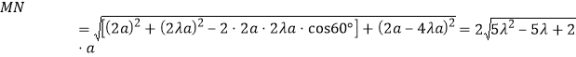 ,
,
∴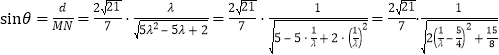
![]() ,
,
当且仅当![]() ,即
,即![]() 时,等号成立,
时,等号成立,
即![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
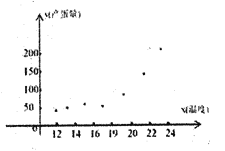
【题目】某研究性学习小组对昼夜温差大小与某种子发芽多少之间的关系进行研究,下面是3月1日至5日每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数的详细记录:
(1)根据3月2日至3月4日的数据,用最小二乘法求出y关于x的线性回归方程;
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均小于2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
参考公式: ,
,![]() .
.