题目内容
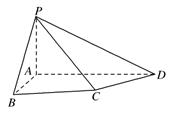
如图,四棱锥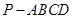 中,
中,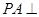 底面
底面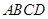 ,四边形
,四边形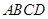 中,
中,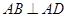 ,
,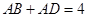 ,
,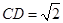 ,
,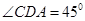 .
.
(Ⅰ)求证:平面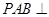 平面
平面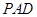 ;
;
(Ⅱ)设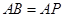 .
.
(ⅰ) 若直线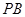 与平面
与平面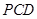 所成的角为
所成的角为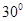 ,求线段
,求线段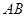 的长;
的长;
(ⅱ) 在线段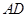 上是否存在一个点
上是否存在一个点 ,使得点
,使得点 到点
到点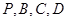 的距离都相等?说明理由.
的距离都相等?说明理由.
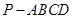 中,
中,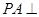 底面
底面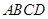 ,四边形
,四边形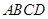 中,
中,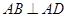 ,
,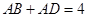 ,
,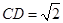 ,
,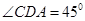 .
.(Ⅰ)求证:平面
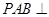 平面
平面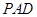 ;
;(Ⅱ)设
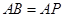 .
.(ⅰ) 若直线
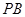 与平面
与平面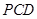 所成的角为
所成的角为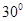 ,求线段
,求线段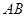 的长;
的长;(ⅱ) 在线段
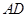 上是否存在一个点
上是否存在一个点 ,使得点
,使得点 到点
到点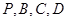 的距离都相等?说明理由.
的距离都相等?说明理由.
(Ⅰ)详见解析;(Ⅱ) 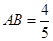 ,不存在
,不存在 点.
点.
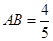 ,不存在
,不存在 点.
点.试题分析:(Ⅰ)先证明线面垂直
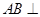 平面
平面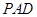 ,再证明面面垂直平面
,再证明面面垂直平面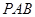 ⊥平面
⊥平面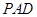 ;(Ⅱ)先建立直角坐标系,设平面
;(Ⅱ)先建立直角坐标系,设平面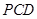 的法向量为
的法向量为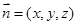 ,利用两向量垂直
,利用两向量垂直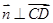 ,
,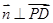 ,列表达式,求出法向量,再由直线
,列表达式,求出法向量,再由直线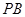 与平面
与平面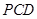 所成的角为
所成的角为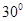 ,得出法向量中的参量;先设存在
,得出法向量中的参量;先设存在 点,找出
点,找出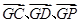 的坐标,利用距离相等,列出表达式,看方程是否有根来判断是否存在
的坐标,利用距离相等,列出表达式,看方程是否有根来判断是否存在 点.
点.试题解析:解法一:
(Ⅰ)证明:因为
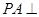 平面
平面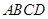 ,
,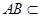 平面
平面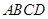 ,
,所以
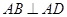 ,又
,又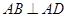 ,
,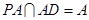 ,
,所以
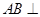 平面
平面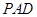 ,又
,又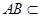 平面
平面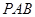 ,
,所以平面
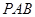 ⊥平面
⊥平面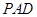 . 3分
. 3分(Ⅱ)以
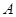 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系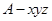 (如图).
(如图).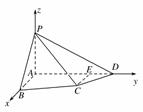
在平面
 内,作
内,作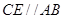 交
交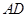 于点
于点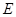 ,则
,则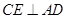 .
.在
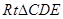 中,
中,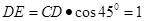 ,
,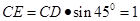 .
.设
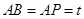 ,则
,则 ,
,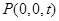 .
.由
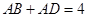 得
得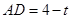 ,
,所以
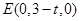 ,
,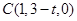 ,
,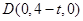 ,
,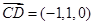 ,
,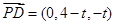 . 5分
. 5分(ⅰ)设平面
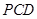 的法向量为
的法向量为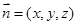 .
.由
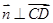 ,
,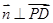 ,得
,得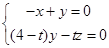
取
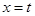 ,得平面
,得平面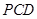 的一个法向量
的一个法向量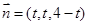 .
.又
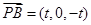 ,故由直线
,故由直线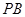 与平面
与平面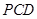 所成的角为
所成的角为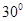 得
得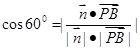 ,即
,即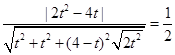 .
.解得
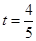 或
或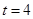 (舍去,因为
(舍去,因为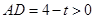 ),所以
),所以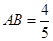 . 7分
. 7分(ⅱ)假设在线段
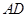 上存在一个点
上存在一个点 ,使得点
,使得点 到点
到点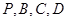 的距离都相等.
的距离都相等.设
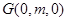 (其中
(其中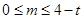 ).
).则
 ,
,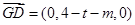 ,
,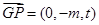 .
.由
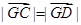 ,得
,得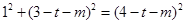 ,
,即
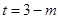 ;①
;①由
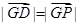 ,得
,得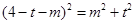 . ②
. ②由①、②消去
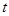 ,化简得
,化简得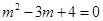 . ③
. ③由于方程③没有实数根,所以在线段
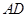 上不存在一个点
上不存在一个点 ,使得点
,使得点 到点
到点 的距离都相等.
的距离都相等.从而,在线段
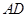 上不存在一个点
上不存在一个点 ,
,使得点
 到点
到点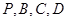 的距离都相等. 12分
的距离都相等. 12分解法二:
(Ⅰ)同解法一:
(Ⅱ)(ⅰ)以
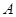 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系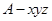 (如图).
(如图).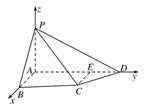
在平面
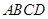 内,作
内,作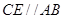 交
交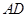 于点
于点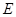 ,
,则
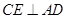 ,
,在
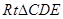 中,
中,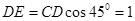 ,
,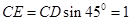 .
.设
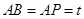 ,则
,则 ,
,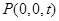 .
.由
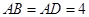 得
得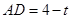 .
.所以
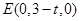 ,
,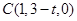 ,
,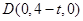 ,
,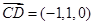 ,
,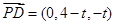 . 5分
. 5分设平面
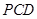 的法向量为
的法向量为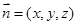 .
.由
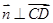 ,
,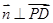 ,得
,得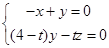
取
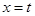 ,得平面
,得平面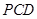 的一个法向量
的一个法向量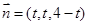 .
.又
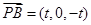 ,故由直线
,故由直线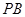 与平面
与平面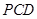 所成的角为
所成的角为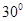 得
得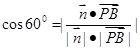 ,即
,即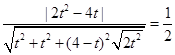 .
.解得
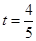 或
或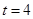 (舍去,因为
(舍去,因为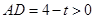 ),所以
),所以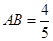 . 7分
. 7分(ⅱ)假设在线段
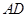 上存在一个点
上存在一个点 ,使得点
,使得点 到点
到点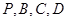 的距离都相等.
的距离都相等.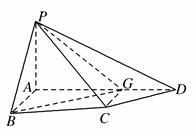
由
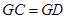 ,得
,得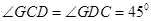 ,
,从而
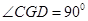 ,即
,即 ,
,所以
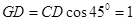 .
.设
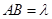 ,则
,则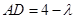 ,
,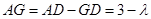 .
.在
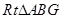 中,
中,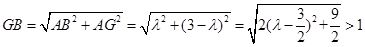 ,这与
,这与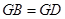 矛盾.
矛盾.所以在线段
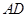 上不存在一个点
上不存在一个点 ,使得点
,使得点 到
到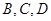 的距离都相等.
的距离都相等.从而,在线段
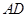 上不存在一个点
上不存在一个点 ,使得点
,使得点 到点
到点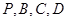 的距离都相等
的距离都相等
练习册系列答案
相关题目
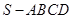 中,底面
中,底面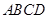 为平行四边形,侧面
为平行四边形,侧面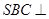 底面
底面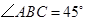 ,
,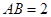 ,
,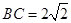 ,
,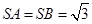 .
.
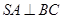 ;
;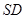 与平面
与平面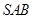 所成角的正弦值.
所成角的正弦值.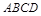 为梯形,
为梯形,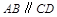 ,
,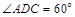 ,四边形
,四边形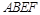 为矩形,且平面
为矩形,且平面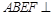 平面
平面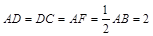 ,点
,点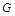 为
为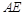 的中点.
的中点.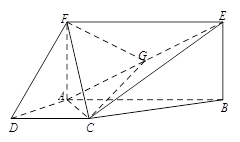
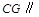 平面
平面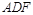 ;
;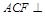 平面
平面 ;
;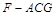 的体积.
的体积.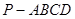 中,
中,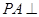 底面
底面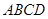 ,面
,面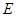 为侧棱
为侧棱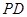 上一点,
上一点,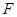 为
为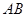 上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.
上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.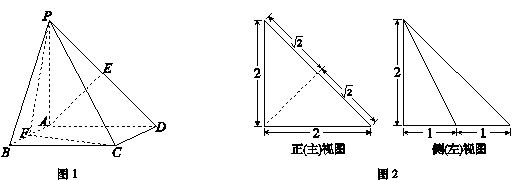
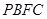 的体积;
的体积;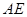 ∥平面
∥平面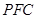 ;
;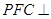 平面
平面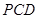 .
.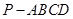 中,
中,  是
是 上的点且
上的点且 为
为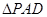 中
中 边上的高.
边上的高. 平面
平面 ;
; ;
; 上是否存在点
上是否存在点 ,使
,使 平面
平面 ?说明理由.
?说明理由.
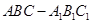 的侧棱与底面
的侧棱与底面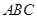 垂直,底面
垂直,底面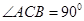 ,侧棱
,侧棱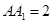 ,
,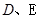 分别是
分别是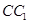 与
与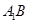 的中点,点
的中点,点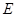 在平面
在平面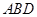 上的射影是
上的射影是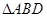 的垂心
的垂心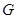
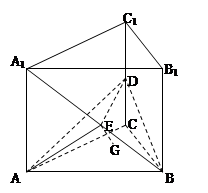
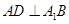 ;
;



 ,装的水恰好占其容积的一半;
,装的水恰好占其容积的一半; 表示水平的桌面,容器一边
表示水平的桌面,容器一边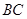 紧贴桌面,沿
紧贴桌面,沿 (如图),设翻转后容器中的水形成的几何体是
(如图),设翻转后容器中的水形成的几何体是 ,翻转过程中水和容器接触面积为
,翻转过程中水和容器接触面积为 ,则下列说法正确的是( )
,则下列说法正确的是( )
 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 、
、 外的一个动点,
外的一个动点, 平面
平面 ,
, ,
, ,
, ,
, .
.
 平面
平面 ;
; 的体积取得最大值,请说明理由并求出这个最大值.
的体积取得最大值,请说明理由并求出这个最大值.