题目内容
四棱锥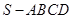 中,底面
中,底面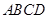 为平行四边形,侧面
为平行四边形,侧面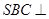 底面
底面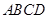 .已知
.已知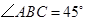 ,
,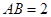 ,
,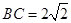 ,
,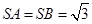 .
.

(Ⅰ)证明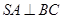 ;
;
(Ⅱ)求直线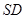 与平面
与平面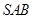 所成角的正弦值.
所成角的正弦值.
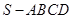 中,底面
中,底面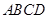 为平行四边形,侧面
为平行四边形,侧面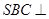 底面
底面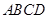 .已知
.已知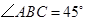 ,
,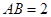 ,
,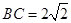 ,
,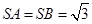 .
.
(Ⅰ)证明
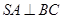 ;
;(Ⅱ)求直线
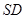 与平面
与平面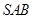 所成角的正弦值.
所成角的正弦值.(Ⅰ)见解析.(Ⅱ)

试题分析:(Ⅰ)通过作
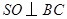 ,垂足为
,垂足为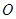 ,连结
,连结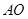 ,根据侧面
,根据侧面 底面
底面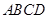 ,得
,得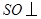 底面
底面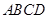 .应用三垂线定理,得
.应用三垂线定理,得 .(Ⅱ)立体几何中的角的计算,一般有两种思路,一是直接法,通过“一作,二证,三计算”等步骤,计算角;二是“间接法”,如利用图形与其投影的面积关系,确定角.本题首先设
.(Ⅱ)立体几何中的角的计算,一般有两种思路,一是直接法,通过“一作,二证,三计算”等步骤,计算角;二是“间接法”,如利用图形与其投影的面积关系,确定角.本题首先设 到平面
到平面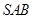 的距离为
的距离为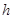 ,根据
,根据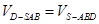 ,求得
,求得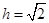 .进一步确定
.进一步确定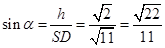 ,将角用反正弦函数表示.
,将角用反正弦函数表示.试题解析:(Ⅰ)作
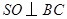 ,垂足为
,垂足为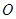 ,连结
,连结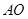 ,由侧面
,由侧面 底面
底面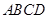 ,得
,得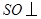 底面
底面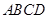 .
.因为
 ,所以
,所以 ,
,又
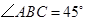 ,故
,故 为等腰直角三角形,
为等腰直角三角形, ,
,由三垂线定理,得
 .
.
(Ⅱ)由(Ⅰ)知
 ,依题设
,依题设 ,
,故
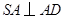 ,由
,由 ,
, ,
,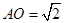 ,得
,得 ,
, .
.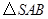 的面积
的面积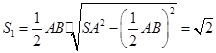 .
.连结
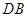 ,得
,得 的面积
的面积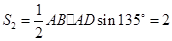
设
 到平面
到平面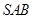 的距离为
的距离为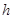 ,由于
,由于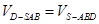 ,得
,得 ,
,解得
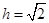 .
.设
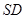 与平面
与平面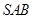 所成角为
所成角为 ,则
,则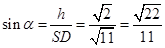 .
.所以,直线
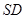 与平面
与平面 所成的角为
所成的角为

练习册系列答案
相关题目
 与
与 均为菱形,设
均为菱形,设 与
与 相交于点
相交于点 ,若
,若 ,且
,且 .
.
 ;
; 的余弦值.
的余弦值.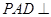 平面
平面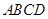 ,
,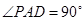 ,且
,且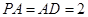 ,
,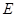 、
、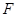 、
、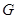 分别是线段
分别是线段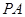 、
、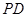 、
、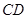 的中点.
的中点.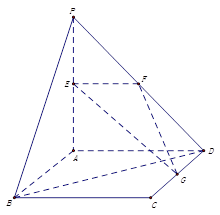
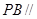 平面
平面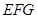 ;
;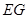 、
、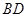 所成角的余弦值.
所成角的余弦值.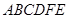 中,四边形
中,四边形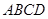 是矩形,
是矩形,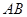 ∥
∥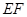 ,
,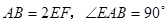 ,平面
,平面 .
.
 点是
点是 中点,求证:
中点,求证: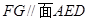 .
.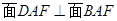 .
.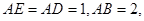 求
求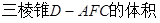 .
.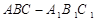 的底面是直角三角形,
的底面是直角三角形, 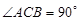 ,侧棱与底面所成角为
,侧棱与底面所成角为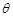 ,点
,点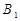 在底面上的射影
在底面上的射影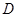 落在
落在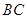 上.
上.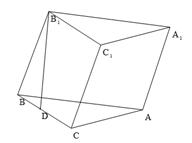
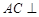 平面
平面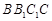 ;
;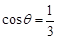 ,且当
,且当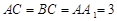 时,求二面角
时,求二面角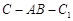 的大小.
的大小.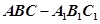 中,
中,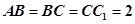 ,
,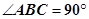 ,D是AC的中点.
,D是AC的中点.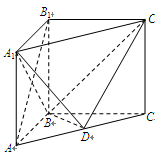
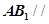 平面
平面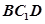 ;
;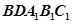 的体积.
的体积.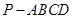 中,
中,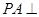 底面
底面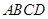 ,四边形
,四边形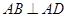 ,
,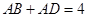 ,
,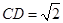 ,
,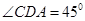 .
.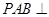 平面
平面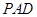 ;
;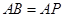 .
.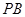 与平面
与平面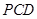 所成的角为
所成的角为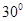 ,求线段
,求线段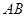 的长;
的长;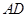 上是否存在一个点
上是否存在一个点 ,使得点
,使得点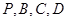 的距离都相等?说明理由.
的距离都相等?说明理由.