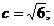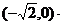题目内容
写出适合下列条件的曲线方程:
(1)a+b=10,c=2
求椭圆的标准方程.
(2)已知双曲线两个焦点分别为F1(-5,0),F2(5,0),双曲线上一点P到F1,F2距离差的绝对值等于6,求双曲线的标准方程.
(1)a+b=10,c=2
| 5 |
(2)已知双曲线两个焦点分别为F1(-5,0),F2(5,0),双曲线上一点P到F1,F2距离差的绝对值等于6,求双曲线的标准方程.
分析:(1)根据椭圆的标准方程与基本量的平方关系,结合题意建立关于a、b、c的方程组,解出a2=36且b2=16,即可得到所求椭圆的标准方程.
(2)设双曲线的标准方程为
-
=1(a>0,b>0),根据双曲线的定义得2a=6,从而得到a=3,结合c=5利用平方关系算出b2=16,即可得出所求双曲线的标准方程.
(2)设双曲线的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
解答:解:(1)当椭圆的焦点在x轴上时,设椭圆的标准方程为
+
=1(a>b>0)
∵
,
解得a2=36,b2=16.
∴椭圆的标准方程为
+
=1;
当椭圆的焦点在y轴上时,同理可得椭圆方程为
+
=1.
综上所述,所求椭圆的标准方程为
+
=1或
+
=1.
(2)∵双曲线焦点在x轴上,
∴设双曲线的标准方程为
-
=1(a>0,b>0)
根据双曲线的定义,可得2a=6且2c=10,
∴a=3,c=5,得b2=c2-a2=16,
因此,所求双曲线的标准方程为
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵
|
解得a2=36,b2=16.
∴椭圆的标准方程为
| x2 |
| 36 |
| y2 |
| 16 |
当椭圆的焦点在y轴上时,同理可得椭圆方程为
| y2 |
| 36 |
| x2 |
| 16 |
综上所述,所求椭圆的标准方程为
| x2 |
| 36 |
| y2 |
| 16 |
| y2 |
| 36 |
| x2 |
| 16 |
(2)∵双曲线焦点在x轴上,
∴设双曲线的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
根据双曲线的定义,可得2a=6且2c=10,
∴a=3,c=5,得b2=c2-a2=16,
因此,所求双曲线的标准方程为
| x2 |
| 9 |
| y2 |
| 16 |
点评:本题给出椭圆、双曲线满足的条件,求它们的标准方程.着重考查了椭圆、双曲线的定义与标准方程等知识,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目