题目内容
写出适合下列条件的椭圆的标准方程
(1) 焦点在x 轴上,a:b=2:1 ,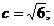
(2)焦点在y轴上,a2+b2=5,且过点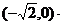
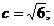
(2)焦点在y轴上,a2+b2=5,且过点
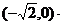
解:(1)∵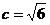 ,
,
∴a2-b2=c2=6,①
又由a:b=2:1代入①
得4b2-b2=6,
∴b2 =2,
∴a2=8.
又∵焦点在x轴上,
∴椭圆的标准方程为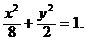
(2)设椭圆的标准方程为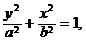
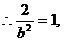
∴b2=2.
又∵a2+b2=5,
∴a2=3,
∴椭圆的标准方程为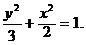
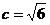 ,
,∴a2-b2=c2=6,①
又由a:b=2:1代入①
得4b2-b2=6,
∴b2 =2,
∴a2=8.
又∵焦点在x轴上,
∴椭圆的标准方程为
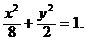
(2)设椭圆的标准方程为
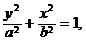
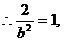
∴b2=2.
又∵a2+b2=5,
∴a2=3,
∴椭圆的标准方程为
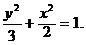

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目