题目内容
在平面直角坐标系 中,已知圆
中,已知圆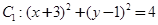 和圆
和圆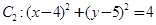 .
.
(1)若直线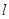 过点
过点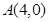 ,且被圆
,且被圆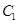 截得的弦长为
截得的弦长为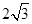 ,求直线
,求直线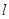 的方程;
的方程;
(2)设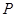 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点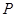 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线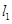 和
和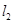 ,它们分别与圆
,它们分别与圆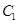 和圆
和圆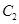 相交,且直线
相交,且直线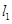 被圆
被圆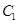 截得的弦长与直线
截得的弦长与直线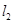 被圆
被圆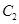 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点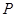 的坐标.
的坐标.
【答案】
(1)  或
或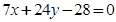 ;(2)
;(2) 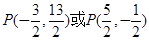 .
.
【解析】
试题分析:(1)涉及到圆的弦长问题,我们一般利用弦心距,弦的一半,相应半径所构成的直角三角形,本题中由弦长为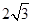 ,半径为2,可求得弦心距为1,此即为圆心到直线的距离,利用点到直线的距离公式,可求得斜率
,半径为2,可求得弦心距为1,此即为圆心到直线的距离,利用点到直线的距离公式,可求得斜率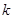 .利用方程思想求
.利用方程思想求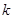 时要注意直线斜率不存在即直线与
时要注意直线斜率不存在即直线与 轴垂直的情形.否则可能漏.(2)由(1)的分析可知直线
轴垂直的情形.否则可能漏.(2)由(1)的分析可知直线 被圆
被圆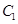 截得的弦长与直线
截得的弦长与直线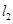 被圆
被圆 截得的弦长相等可得圆心
截得的弦长相等可得圆心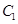 到直线
到直线 的距离与圆心
的距离与圆心 到直线
到直线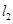 距离相等,所以我们可设
距离相等,所以我们可设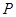 点坐标为
点坐标为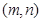 ,直线
,直线 的方程分别为
的方程分别为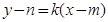 ,
, ,利用圆心
,利用圆心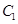 到直线
到直线 的距离与圆心
的距离与圆心 到直线
到直线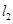 距离相等列出关于
距离相等列出关于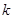 的方程,再转化为关于
的方程,再转化为关于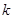 的方程有无穷解问题,从而得解.
的方程有无穷解问题,从而得解.
试题解析:(1)设直线 的方程为
的方程为 ,即
,即
由垂径定理得圆心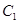 到直线
到直线 的距离
的距离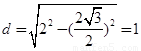
结合点到直线的距离公式得
所求直线 的方程为
的方程为 或
或 ,即
,即 或
或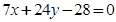
(2)设点 ,直线
,直线 的方程分别为
的方程分别为
即
由题意可知圆心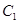 到直线
到直线 的距离等于
的距离等于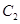 到直线
到直线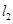 的距离
的距离
即 ,化简得
,化简得 ,关于
,关于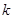 的方程由无穷多解,则有
的方程由无穷多解,则有
 ,故
,故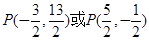 .
.
考点:(1)点到直线距离公式;(2)方程解的个数问题.

练习册系列答案
相关题目