题目内容
下面四个命题中正确的是:( )
A.“直线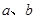 不相交”是“直线 不相交”是“直线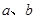 为异面直线”的充分非必要条件 为异面直线”的充分非必要条件 |
B.“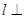 平面 平面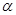 ”是“直线 ”是“直线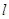 垂直于平面 垂直于平面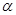 内无数条直线”的充要条件 内无数条直线”的充要条件 |
C.“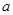 垂直于 垂直于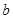 在平面 在平面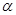 内的射影”是“直线 内的射影”是“直线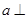 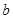 ”的充分非必要条件 ”的充分非必要条件 |
D.“直线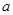 平行于平面 平行于平面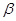 内的一条直线”是“直线 内的一条直线”是“直线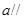 平面 平面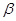 ”的必要非充分条件 ”的必要非充分条件 |
D
分析:根据平行线与异面线的定义判断出A错;据直线与平面垂直的判定定理判断出B错;根据两直线射影垂直两直线不一定垂直判断出C错;据直线与平面平行的性质定理判断出D正确。
解答:
对于A,“直线a、b不相交”时,“直线a、b为异面直线或平行直线”,故A错;
对于B,“l⊥平面α”能推出“直线l垂直于平面α内无数条直线”,反之“直线l垂直于平面α内无数条直线”推不出“l⊥平面α”所以“l⊥平面α”是“直线l垂直于平面α内无数条直线”的充分不必要条件,故B错;
对于C,“a垂直于b在平面α内的射影”时,则有“直线a⊥b或a,b斜交”,故C错;
对于D,当“直线a平行于平面β内的一条直线”时,若a在面内,则推不出“直线a∥平面β”;反之若“直线a∥平面β”,则有经过a作一平面与已知平面相交,则a平行于交线,所以D正确;故选D。
点评:本题考查直线与平面平行的性质;直线与平面垂直的判定,属于基础题。

练习册系列答案
相关题目
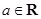 ,则“
,则“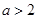 ”是“
”是“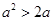 ”的( )
”的( )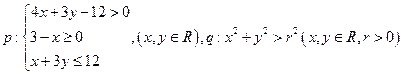 ,若非
,若非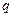 是非
是非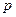 的充分不必要条件,那么
的充分不必要条件,那么 条件,
条件,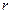 的取值范围是
的取值范围是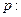 若
若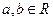 ,则
,则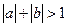 是
是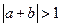 的充分而不必要条件;
的充分而不必要条件;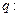 函数
函数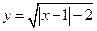 的定义域是
的定义域是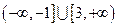 ,则( )
,则( )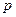 或
或 ”为假
”为假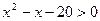 ,q:
,q: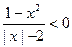 ,则
,则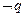 是
是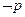 的( )
的( )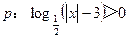 ,
,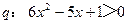 ,则
,则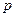 是
是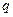 的( )
的( )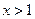 ”是“
”是“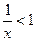 ”的 条件.(充分不必要、必要不充分、充要、既不充分又不必要)
”的 条件.(充分不必要、必要不充分、充要、既不充分又不必要)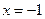 ”是“
”是“ ”的必要不充分条件
”的必要不充分条件
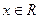 ,
,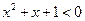 ”的否定是“
”的否定是“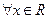 ,
,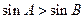 是
是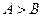 的充要条件
的充要条件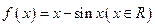 有3个零点
有3个零点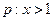 ,条件
,条件 ,则
,则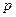 是
是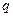 成立的 ( )
成立的 ( )