题目内容
已知二次函数f(x)=x2+ax(
 ).
).
(1)若函数y=f(sinx+ cosx)(
cosx)(
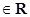 )的最大值为
)的最大值为 ,求f(x)的最小值;
,求f(x)的最小值;
(2)当a>2时,求证:f(sin2xlog2sin2x+cos2xlog2cos2x) 1–a.其中x∈R,x¹kp且x¹kp
1–a.其中x∈R,x¹kp且x¹kp (k∈Z).
(k∈Z).
【答案】
(1)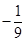 ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)先求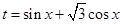 的值域,再讨论a的范围,根据最大值,求最小值;(2)利用导数先求sin2xlog2sin2x+cos2xlog2cos2x的值域,再根据二次函数求结论.
的值域,再讨论a的范围,根据最大值,求最小值;(2)利用导数先求sin2xlog2sin2x+cos2xlog2cos2x的值域,再根据二次函数求结论.
试题解析:(1)令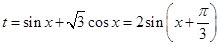 ,
,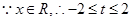 , 2分
, 2分
 ,当a<0时,t=–2时,
,当a<0时,t=–2时,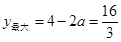 ,
,
解得: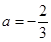
此时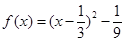 ,
,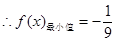 .
2分
.
2分
当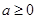 时,t=2时,
时,t=2时,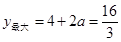 ,解得:
,解得: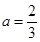
此时,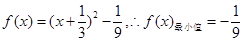
综合上述,条件满足时,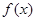 的最小值为
的最小值为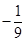 2分
2分
(2)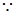 x∈R,
x∈R,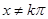 且
且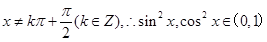
又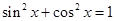 ,故设
,故设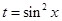 ,则有
,则有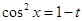
设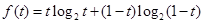 (其中t∈(0,1))
2分
(其中t∈(0,1))
2分
 2分
2分
令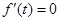 ,得
,得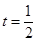
当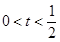 时,
时,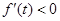 ,所以
,所以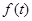 在(0,
在(0,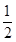 )单调递减,
)单调递减,
当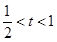 时,
时,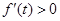 ,所以
,所以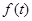 在(
在(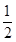 ,1)单调递增,
,1)单调递增,
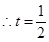 时
时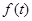 取最小值等于
取最小值等于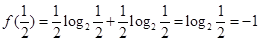
即有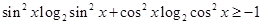 3分
3分
当a>2时,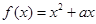 的对称轴
的对称轴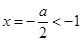 ,
,
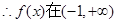 上单调递增,
上单调递增,
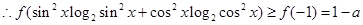 2分
2分
考点:1、利用导数求函数的单调性;2、二次函数;3、导数与二次函数、三角函数的综合应用.

练习册系列答案
相关题目