题目内容
已知tan2α=-
,tan(α-β)=
,则tan(α+β)( )
| 3 |
| 4 |
| 1 |
| 2 |
分析:根据α+β=2α-(α-β),利用两角差的正切公式,计算可得结论.
解答:解:∵α+β=2α-(α-β),tan2α=-
,tan(α-β)=
,
∴tan(α+β)=tan[2α-(α-β)]=
=
=-2
故选A.
| 3 |
| 4 |
| 1 |
| 2 |
∴tan(α+β)=tan[2α-(α-β)]=
| tan2α-tan(α-β) |
| 1+tan2αtan(α-β) |
-
| ||||
1-
|
故选A.
点评:本题考查两角差的正切公式的运用,考查学生的计算能力,解题的关键是利用α+β=2α-(α-β).

练习册系列答案
相关题目
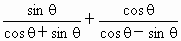 的值是______.
的值是______.
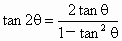 )
)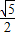 ,且3π<2θ<4π.
,且3π<2θ<4π.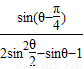 .
.