题目内容
(2012•江门一模)已知f(x)=x2,g(x)=lnx,直线l:y=kx+b(常数k、b∈R)使得函数y=f(x)的图象在直线l的上方,同时函数y=g(x)的图象在直线l的下方,即对定义域内任意x,lnx<kx+b<x2恒成立.
试证明:
(1)k>0,且-lnk-1<b<-
;
(2)“e-
<k<e”是“lnx<kx+b<x2”成立的充分不必要条件.
试证明:
(1)k>0,且-lnk-1<b<-
| k2 |
| 4 |
(2)“e-
| 1 |
| 2 |
分析:(1)由lnx<kx+b恒成立,结合对数函数的性质,得k>0.由kx+b<x2恒成立,结合根的判别式可得b<-
.再根据lnx<kx+b恒成立,讨论讨论函数h(x)=kx+b-lnx的单调性与最小值,得到h(
)=1+b+lnk>0,从而得原不等式成立.
(2)根据幂函数与对数函数单调性,可得k应介于曲线f(x)=x2与g(x)=lnx的两个交点的横坐标之间.通过计算比较f(e-
)与g(e-
)、f(e)与g(e)的大小,可得区间(e-
,e)恰好位于两交点横坐标之间,从而证出本题的充分不必要条件.
| k2 |
| 4 |
| 1 |
| k |
(2)根据幂函数与对数函数单调性,可得k应介于曲线f(x)=x2与g(x)=lnx的两个交点的横坐标之间.通过计算比较f(e-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: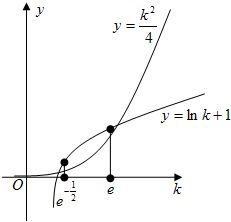 解:(1)根据题意,得
解:(1)根据题意,得
对任意x,lnx<kx+b,所以k>
…(1分),
因为k、b是常数,所以当x充分大时,lnx>b,
从而k>
>0…(2分).
因为kx+b<x2即x2-kx-b>0恒成立,
所以△=(-k)2+4b<0,得b<-
…(4分).
因为lnx<kx+b即kx+b-lnx>0恒成立,
设h(x)=kx+b-lnx,则h'(x)=k-
…(5分),
由h'(x)=0得x=
>0,
∴0<x<
时,h'(x)<0,h(x)单调递减;x>
时时,h'(x)<0,h(x)单调递增…(7分),
所以h(x)的极小值从而也是最小值为h(
)=1+b-ln
=1+b+lnk…(8分),
因为kx+b-lnx>0恒成立,所以h(
)=1+b+lnk>0,即b>-lnk-1,从而-lnk-1<b<-
成立;…(9分).
(2)由(1)知-lnk-1<-
,从而
<lnk+1,其中k是正数…(10分),
如图,根据幂函数与对数函数单调性,
可得k应介于曲线f(x)=x2与g(x)=lnx的两个交点的横坐标之间,
设这两个交点横坐标分别为x1、x2,且x1<x2.…(11分),
因为k=e-
时,
<
=lnk+1,k=e时,
=
<2=lnk+1…(13分),
所以(e-
,e)是(x1,x2)的真子集,
由此可得:“e-
<k<e”是“lnx<kx+b<x2”成立的充分不必要条件.…(14分).
 解:(1)根据题意,得
解:(1)根据题意,得对任意x,lnx<kx+b,所以k>
| lnx-b |
| x |
因为k、b是常数,所以当x充分大时,lnx>b,
从而k>
| lnx-b |
| x |
因为kx+b<x2即x2-kx-b>0恒成立,
所以△=(-k)2+4b<0,得b<-
| k2 |
| 4 |
因为lnx<kx+b即kx+b-lnx>0恒成立,
设h(x)=kx+b-lnx,则h'(x)=k-
| 1 |
| x |
由h'(x)=0得x=
| 1 |
| k |
∴0<x<
| 1 |
| k |
| 1 |
| k |
所以h(x)的极小值从而也是最小值为h(
| 1 |
| k |
| 1 |
| k |
因为kx+b-lnx>0恒成立,所以h(
| 1 |
| k |
| k2 |
| 4 |
(2)由(1)知-lnk-1<-
| k2 |
| 4 |
| k2 |
| 4 |
如图,根据幂函数与对数函数单调性,
可得k应介于曲线f(x)=x2与g(x)=lnx的两个交点的横坐标之间,
设这两个交点横坐标分别为x1、x2,且x1<x2.…(11分),
因为k=e-
| 1 |
| 2 |
| k2 |
| 4 |
| 1 |
| 2 |
| k2 |
| 4 |
| e2 |
| 4 |
所以(e-
| 1 |
| 2 |
由此可得:“e-
| 1 |
| 2 |
点评:本题给出介于两个函数图象之间的一条线段对应的函数,求证参数的取值范围并证明充分条件,着重考查了基本初等函数、利用导数研究函数的单调性与最值和充分必要条件的证明等知识,属于中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 (2012•江门一模)(几何证明选讲选做题)
(2012•江门一模)(几何证明选讲选做题)
 (2012•江门一模)如图,某几何体的正视图和侧视图都是对角线长分别为4和3的菱形,俯视图是对角线长为3的正方形,则该几何体的体积为( )
(2012•江门一模)如图,某几何体的正视图和侧视图都是对角线长分别为4和3的菱形,俯视图是对角线长为3的正方形,则该几何体的体积为( ) (2012•江门一模)如图,四边形ABCD中,AB=5,AD=3,cosA=
(2012•江门一模)如图,四边形ABCD中,AB=5,AD=3,cosA=