题目内容
（本小题满分12分）某工厂家具车间造A，B型两类桌子，每张桌子需木工和漆工两道工序完成．已知木工做一张A，B型桌子分别需要1 h和2 h，漆工油漆一张A，B型桌子分别需要3 h和1 h；又知木工、漆工每天工作分别不得超过8 h和9 h，而工厂造一张A，B型桌子分别获利润2千元和3千元，试问：工厂每天应生产A，B型桌子各多少张，才能获得最大利润？
【答案】
解：设每天生产A型桌子x张，B型桌子y张，则4分
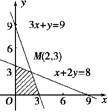
目标函数为z=2x+3y.作出可行域如图所示． 8分
把直线l：2x+3y=0向右上方平移至l′的位置时，直线经过可行域上的点M，且与原点距离最大，此时z=2x+3y取最大值，解方程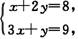
得M的坐标为(2,3)． 11分
故每天应生产A型桌子2张、B型桌子3张才能获得最大利润． 12分
【解析】略
练习册系列答案
字词句段篇系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
