题目内容
如图，设平面AC和BD相交于BC，它们所成的一个二面角为45°，P为平面AC内的一点，Q为面BD内的一点，已知直线MQ是直线PQ在平面BD内的射影，并且M在BC上又设PQ与平面BD所成的角为β，∠CMQ=θ（0°＜θ＜90°），线段PM的长为a，求线段PQ的长．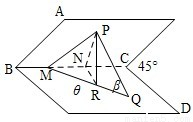
【答案】分析：过点P作平面BD的垂线，垂足为R，由PQ与平面BD所成的角为β，要求PQ，可根据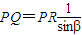
，故我们要先求PR值，而由二面角的平面角为45°，我们可得NR=PR，故我们要先根据MR=
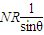，及a2=PR2+MR2，求出NR的值．
解答：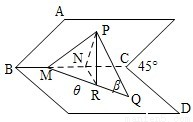
解：自点P作平面BD的垂线，垂足为R，
由于直线MQ是直线PQ在平面BD内的射影，
所以R在MQ上，过R作BC的垂线，设垂足为N，
则PN⊥BC（三垂线定理
因此∠PNR是所给二面角的平面角，所以∠PNR=45°
由于直线MQ是直线PQ在平面BD内的射影，所以∠PQR=β
在Rt△PNR中，NR=PRcot45°，所以NR=PR．
在Rt△MNR中，MR=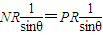
，
在Rt△PMR中，
，
又已知0°＜θ＜90°，所以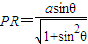
．
在Rt△PRQ中，
．
故线段PQ的长为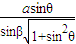
．
点评：本题考查的知识点是平面与平面间的位置关系，二面角，解三角形，根据已知条件由未知的结论利用分析法寻求解题思路是解题的关键．
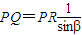，故我们要先求PR值，而由二面角的平面角为45°，我们可得NR=PR，故我们要先根据MR=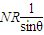，及a2=PR2+MR2，求出NR的值．解答：
解：自点P作平面BD的垂线，垂足为R，由于直线MQ是直线PQ在平面BD内的射影，
所以R在MQ上，过R作BC的垂线，设垂足为N，
则PN⊥BC（三垂线定理
因此∠PNR是所给二面角的平面角，所以∠PNR=45°
由于直线MQ是直线PQ在平面BD内的射影，所以∠PQR=β
在Rt△PNR中，NR=PRcot45°，所以NR=PR．
在Rt△MNR中，MR=
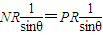，在Rt△PMR中，
，又已知0°＜θ＜90°，所以
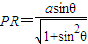．在Rt△PRQ中，
．故线段PQ的长为
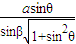．点评：本题考查的知识点是平面与平面间的位置关系，二面角，解三角形，根据已知条件由未知的结论利用分析法寻求解题思路是解题的关键．
练习册系列答案
相关题目
在A，B，C，D四小题中只能选做2题，每题10分，共计20分．
如图，Rt△ABC中，∠ABC=90°，BA=BC=2，分别过A、C作平面ABC的垂线AA′和CC′，AA′=h1，CC′=h2，且h1＞h2，连接A′C和AC′交于点P．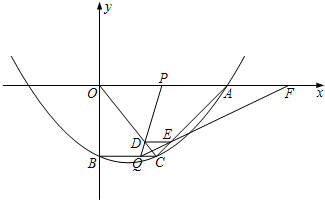
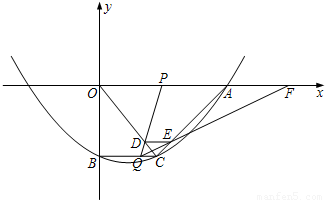
如图，在平面直角坐标系xoy中，抛物线y=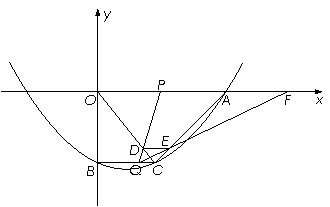
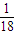x 2－
x－10与x轴的交点为A，与y轴的交点为点B，过点B作x轴的平行线BC，交抛物线于点C，连结AC．现有两动点P，Q分别从O，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位的速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动．线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x轴于点F．设动点P，Q移动的时间为t(单位：秒)
）时，△PQF的面积是否总为定值？若是，求出此定值；若不是，请说明理由；
x2-
x-10与x轴的交点为A，与y轴的交点为点B，过点B作x轴的平行线BC，交抛物线于点C，连接AC、现有两动点P，Q分别从O，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位的速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动．线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x轴于点F．设动点P，Q移动的时间为t（单位：秒）
）时，△PQF的面积是否总为定值？若是，求出此定值；若不是，请说明理由；