题目内容
 在直四棱柱ABCD-A1B1C1D1中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,C1O与平面ABCD所成的角为60°.
在直四棱柱ABCD-A1B1C1D1中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,C1O与平面ABCD所成的角为60°.(1)求三棱锥A1-BCD的体积;
(2)求异面直线C1O与CD1所成角的大小(结果用反三角函数值表示).
分析:(1)根据题意可得∠C1OC=60°,求出CC1的值,代入三棱锥的体积公式运算求得结果.
(2)解法一:设AD1与A1D相交于M,则∠MOC1就是异面直线C1O与CD1所成的角,由余弦定理求得cos∠MOC1 的值,
即可求得∠MOC1的值.
解法二:建立空间直角坐标系,求出
和
的坐标,利用两个向量的夹角公式求出
和
的夹角,
即可得到异面直线C1O与CD1所成的角.
(2)解法一:设AD1与A1D相交于M,则∠MOC1就是异面直线C1O与CD1所成的角,由余弦定理求得cos∠MOC1 的值,
即可求得∠MOC1的值.
解法二:建立空间直角坐标系,求出
| OC |
| CD1 |
| OC |
| CD1 |
即可得到异面直线C1O与CD1所成的角.
解答: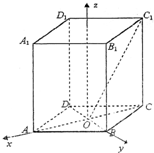 解:(1)∵CC1⊥ABCD,∴∠C1OC就是C1O与平面ABCD所成的角,
解:(1)∵CC1⊥ABCD,∴∠C1OC就是C1O与平面ABCD所成的角,
…(2分)
在正△ABD中,AO=
=OC,∴CC1=
tan60°=3,…(4分)
∴VA-BCD=
•AA1•S△BCD=
,
∴三棱锥A1-BCD体积为
.…(6分)
(2)解法一:设AD1与A1D相交于M,
连OM、CD1,则OM∥CD1,
∴∠MOC1就是异面直线C1O与CD1所成的角.…(8分)
连C1M,在△OC1M中,OC1=2
,OM=
CD1=
,C1M=
-
,cos∠MOC1=
=
=
…(12分)
∴∠MOC1=arccos
,
∴异面直线C1O与CD1所成角为 arccos
.…(14分)
解法二:如图建立空间直角坐标系,则
O(0,0,0),C1(-
,0,3),
∴
=(-
,0,3)…(8分)C(-
,0,0),D(0,-1,3),
∴
=(
,-1,3)…(10分)
设异面直线C1O与CD1所成的角为θ
∴cosθ=
=
,∴θ=arccos
∴异面直线C1O与CD1所成角为 arrcos
…(14分)
 解:(1)∵CC1⊥ABCD,∴∠C1OC就是C1O与平面ABCD所成的角,
解:(1)∵CC1⊥ABCD,∴∠C1OC就是C1O与平面ABCD所成的角,…(2分)
在正△ABD中,AO=
| 3 |
| 3 |
∴VA-BCD=
| 1 |
| 3 |
| 3 |
∴三棱锥A1-BCD体积为
| 3 |
(2)解法一:设AD1与A1D相交于M,
连OM、CD1,则OM∥CD1,
∴∠MOC1就是异面直线C1O与CD1所成的角.…(8分)
连C1M,在△OC1M中,OC1=2
| 3 |
| 1 |
| 2 |
| ||
| 2 |
|
| ||
| 2 |
12+
| ||||||
2×2
|
| 6 | ||
2
|
| ||
| 13 |
∴∠MOC1=arccos
| ||
| 13 |
∴异面直线C1O与CD1所成角为 arccos
| ||
| 13 |
解法二:如图建立空间直角坐标系,则
O(0,0,0),C1(-
| 3 |
∴
| OC |
| 3 |
| 3 |
∴
| CD1 |
| 3 |
设异面直线C1O与CD1所成的角为θ
∴cosθ=
| 6 | ||||
|
| ||
| 13 |
| ||
| 13 |
∴异面直线C1O与CD1所成角为 arrcos
| ||
| 13 |
点评:本题考查球三棱锥的体积,异面直线所成的角的定义和求法,找出两异面直线所成的角,是解题的关键.

练习册系列答案
相关题目
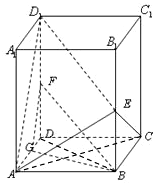 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.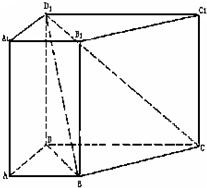 在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.
在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.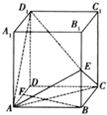 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=
如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE= 在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.
在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.