题目内容
(14分)已知函数g(x)=
在
上为增函数，且
，f(x)=mx-
(I)求
的值；
(II)若f(x)-g(x)在上为单调函数，求m的取值范围；
（Ⅲ）设
，若在
上至少存在一个
，使得
成立，求m的取值范围.
解：（1）由题意：
在
上恒成立，即
，
在上恒成立，
只需sin
…………（4分）
(2) 由(1),得f(x)-g(x)=mx-
,
,由于f(x)-g(x)在其定义域内为单调函数，则
在上恒成立，即
在上恒成立，故
，综上，m的取值范围是
…………（8分）
（3）构造函数F(x)=f(x)-g(x)-h(x),
,
当
由
得，
，所以在
上不存在一个
，使得
； …………（11分）
当m>0时，
，因为，所以
在上恒成立，故F(x)在上单调递增，
，故m的取值范围是
（14分）
练习册系列答案
名校课堂系列答案
相关题目
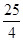）ex（a>0），若存在x1，x2∈[0，4]使得|f（x1）-g（x2）|<1成立，求a的取值范围．
．
的单调区间；
的图像在点
处的切线的倾斜角为
，问：
在什么范围取值时，对于任意的
，函数g(x)=x3 + x2
在区间
上总存在极值？
时，设函数
，若在区间
上至少存在一个
，
成立，试求实数
的取值范围．
，求函数φ (x)的单调区间；