Question

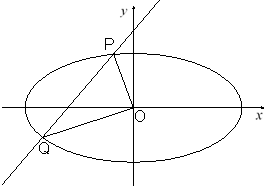在直角坐标系xOy中，点M到点F₁(-

3

，0)、F₂(

3

，0)的距离之和是4，点M的轨迹是C，直线l：y=kx+

2

与轨迹C交于不同的两点P和Q．
（Ⅰ）求轨迹C的方程；
（Ⅱ）是否存在常数k，使以线段PQ为直径的圆过原点O？若存在，求出k的值；若不存在，请说明理由．

Answer 1

分析：（Ⅰ）直接结合条件利用定义得M的轨迹C是长轴长为4，焦点在x轴上焦距为2

3

的椭圆，即可求轨迹C的方程；
（Ⅱ）先把直线方程与曲线方程联立，得到关于点P和Q坐标之间的等式，再代入以线段PQ为直径的圆过原点O的等价结论x₁x₂+y₁y₂=0即可求出k的值．

解答：解：（1）∵点M到(-

3

，0)，(

3

，0)的距离之和是4，
∴M的轨迹C是长轴长为4，焦点在x轴上焦距为2

3

的椭圆，
其方程为

x2

4

+y2=1．（4分）
（2）将y=kx+

2

，代入曲线C的方程，整理得(1+4k2)x2+8

2

kx+4=0．①（6分）
设P（x₁，y₁），Q（x₂，y₂），由方程①，得x1+x2=-

8 2 k

1+4k2

，x1x2=

4

1+4k2

．②（8分）
又y1•y2=(kx1+

2

)(kx2+

2

)=k2x1x2+

2

k(x1+x2)+2．③（9分）
若以PQ为直径的圆过原点，则

OP

•

OQ

=0，所以x₁x₂+y₁y₂=0，（10分）
将②、③代入上式，解得k=±

6

2

．（12分）
又因k的取值应满足△＞0，即4k²-1＞0（*），将k=±

6

2

代入（*）式知符合题意．（13分）

点评：本题综合考查了直线与椭圆的位置关系以及轨迹方程的求法．直线与圆锥曲线的位置关系，由于集中交汇了直线，圆锥曲线两章的知识内容，综合性强，能力要求高，还涉及到函数，方程，不等式，平面几何等许多知识，可以有效的考查函数与方程的思想，数形结合的思想，分类讨论的思想和转化化归的思想，因此，这一部分内容也成了高考的热点和重点．