题目内容
【题目】已知函数f(x)=ax﹣lnx,F(x)=ex+ax,其中x>0.
(1)若a<0,f(x)和F(x)在区间(0,ln3)上具有相同的单调性,求实数a的取值范围;
(2)设函数h(x)=x2﹣f(x)有两个极值点x1、x2 , 且x1∈(0, ![]() ),求证:h(x1)﹣h(x2)>
),求证:h(x1)﹣h(x2)> ![]() ﹣ln2.
﹣ln2.
【答案】
(1)解:f′(x)=a﹣ ![]() =
= ![]() ,F′(x)=ex+a,x>0,
,F′(x)=ex+a,x>0,
∵a<0,f′(x)<0在(0,+∞)上恒成立,即f(x)在(0,+∞)上单调递减,
当﹣1≤a<0时,F′(x)>0,即F(x)在(0,+∞)上单调递增,不合题意;
当a<﹣1时,由F′(x)>0,得x>ln(﹣a),由F′(x)<0,得0<x<ln(﹣a),
∴F(x)的单调减区间为(0,ln(﹣a)),单调增区间为(ln(﹣a),+∞).
∵f(x)和F(x)在区间(0,ln3)上具有相同的单调性,
∴ln(﹣a)≥ln3,解得a≤﹣3,
综上,a的取值范围是(﹣∞,﹣3]
(2)解:证明:h(x)=x2﹣ax+lnx,∴h′(x)= ![]() ,(x>0),
,(x>0),
x1x2= ![]() ,则x2=
,则x2= ![]() ,
,
h(x1)﹣h(x2)=lnx1+x12﹣ax1﹣lnx2﹣x22+ax2
=ln ![]() +[x1+x2﹣2(x1+x2)(x1﹣x2)
+[x1+x2﹣2(x1+x2)(x1﹣x2)
=ln2+2lnx1﹣x12+ ![]() ,
,
令g(x1)=ln2+2lnx1﹣x12+ ![]() ,
,
则g′(x)= ![]() ﹣2x1﹣
﹣2x1﹣ ![]() =﹣
=﹣ 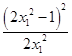 ,
,
∵0<x1< ![]() ,∴g′(x1)<0,
,∴g′(x1)<0,
∴g(x1)在(0, ![]() )上单调递减,
)上单调递减,
∴g(x1)>g( ![]() ),而g(
),而g( ![]() )=
)= ![]() ﹣ln2,
﹣ln2,
即g(x1)> ![]() ﹣ln2,
﹣ln2,
∴h(x1)﹣h(x2)> ![]() ﹣ln2
﹣ln2
【解析】(1)求出函数的导数,通过讨论a的范围,结合函数的单调性确定a的范围即可;(2)先求出h(x1)﹣h(x2)=ln2+2lnx1﹣x12+ ![]() ,构造函数,求出函数的导数,得到函数的单调区间,求出函数的最小值,从而证明结论.
,构造函数,求出函数的导数,得到函数的单调区间,求出函数的最小值,从而证明结论.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】医学上所说的“三高”通常是指血脂增高、血压增高、血糖增高等疾病.为了解“三高”疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将列联表补充完整;
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(2)能否在犯错误的概率不超过0.005的前提下认为患“三高”疾病与性别有关? 下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() .
.
【题目】如表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据,根据表提供的数据,求出y关于x的线性回归方程为 ![]() =0.7x+0.35,则下列结论错误的是( )
=0.7x+0.35,则下列结论错误的是( )
x | 3 | 4 | 5 | 6 |
y | 2.5 | t | 4 | 4.5 |
A.产品的生产能耗与产量呈正相关
B.t的取值必定是3.15
C.回归直线一定过点(4,5,3,5)
D.A产品每多生产1吨,则相应的生产能耗约增加0.7吨