题目内容
已知点P1(a1,b1),P2(a2,b2),…,Pn(an,bn)(n为正整数)都在函数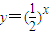 的图象上,且数列{an} 是a1=1,公差为d的等差数列.
的图象上,且数列{an} 是a1=1,公差为d的等差数列.(1)证明:数列{bn} 是公比为
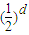 的等比数列;
的等比数列;(2)若公差d=1,以点Pn的横、纵坐标为边长的矩形面积为cn,求最小的实数t,若使cn≤t(t∈R,t≠0)对一切正整数n恒成立;
(3)对(2)中的数列{an},对每个正整数k,在ak与ak+1之间插入2k-1个3(如在a1与a2之间插入2个3,a2与a3之间插入21个3,a3与a4之间插入22个3,…,依此类推),得到一个新的数列{dn},设Sn是数列{dn}的前n项和,试求S1000.
【答案】分析:(1)根据题中已知条件以及等差数列的基本性质,先求出bn的通项公式,然后证明为常数即可证明;
(2)先求出bn的通项公式,然后求出cn的表达式,可知数列cn从第二项起随n增大而减小,故cn≤c2,即t=c2,便可求出t的最小值;
(3)根据题意先求出dn的表达式,然后求出Sn的表达式,继而可以求得S1000的值.
解答:解:(1)由已知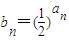 ,(1分)
,(1分)
所以,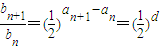 (常数),(4分)
(常数),(4分)
所以数列bn是等比数列.(5分)
(2)公差d=1,则an=n,得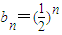 ,
,
∴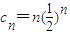 ,(7分)
,(7分)
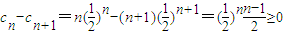 ,
,
∴c1=c2>c3>c4>cn,
数列cn从第二项起随n增大而减小(10分)
∴又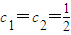 ,则
,则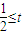 .最小的实数t等于
.最小的实数t等于 (12分)
(12分)
(3)∵an=n,
∴数列dn中,从第一项a1开始到ak为止(含ak项),
共有k+2+21++2k-2=k+2k-1-1项,(14分)
k=10时k+2k-1-1=521(15分)
k=11时k+2k-1-1=1034>1000(16分)
∴S1000=(1+2+10)+990×3=3025(18分)
点评:本题考查了等差数列和等比数列的基本性质以及函数的综合应用,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.
(2)先求出bn的通项公式,然后求出cn的表达式,可知数列cn从第二项起随n增大而减小,故cn≤c2,即t=c2,便可求出t的最小值;
(3)根据题意先求出dn的表达式,然后求出Sn的表达式,继而可以求得S1000的值.
解答:解:(1)由已知
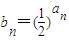 ,(1分)
,(1分)所以,
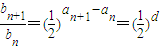 (常数),(4分)
(常数),(4分)所以数列bn是等比数列.(5分)
(2)公差d=1,则an=n,得
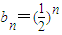 ,
,∴
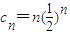 ,(7分)
,(7分)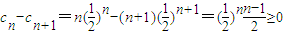 ,
,∴c1=c2>c3>c4>cn,
数列cn从第二项起随n增大而减小(10分)
∴又
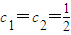 ,则
,则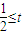 .最小的实数t等于
.最小的实数t等于 (12分)
(12分)(3)∵an=n,
∴数列dn中,从第一项a1开始到ak为止(含ak项),
共有k+2+21++2k-2=k+2k-1-1项,(14分)
k=10时k+2k-1-1=521(15分)
k=11时k+2k-1-1=1034>1000(16分)
∴S1000=(1+2+10)+990×3=3025(18分)
点评:本题考查了等差数列和等比数列的基本性质以及函数的综合应用,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 ,其中{an}、{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.
,其中{an}、{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.