题目内容

求实数x分别取什么值时，复数z=x2+x-6+（x2-2x-15）i对应的点Z在：
（1）第三象限；
（2）直线x-y-3=0．
分析：（1）当Z落在第三象限内，列出不等式组，解不等式组可得x的范围．
（2）可得Z坐标，代入直线方程，解之即可；
解答：解：（1）由题意可知复数z=x2+x-6+（x2-2x-15）i对应的点Z（x2+x-6，x2-2x-15），
落在第三象限内，
∴
x2-2x-15＜0
x2+x-6＜0
，
解得x∈（-3，2）．
（2）当Z落在直线x-y-3=0时，
可得x2+x-6-（x2-2x-15）-3=0
解之可得x=2．
点评：本题考查复数的代数形式的表示方法及几何意义，属基础题．
练习册系列答案
相关题目
已知命题p：?x∈[1，12]，x2-a≥0．命题q：?x0∈R，使得x
 
2
0
+（a-1）x0+1＜0．
（1）若p或q为真，p且q为假，求实数a的取值范围． 
（2）实数m分别取什么值时，复数z=m+1+（m-1）i是 ①实数？②虚数？③纯虚数？
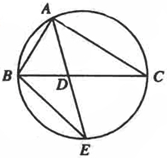精英家教网选作题：考生任选一题作答，如果多做，则按所做的第一题计分．
A 如图，△ABC的角平分线AD的延长线交它的外接圆于点E．
（I）证明：△ABE∽△ADC
（II）若△ABC的面积S=
1
2
AD•AE，求∠BAC的大小．
B 已知曲线C1：
x=-4+cost
y=3+sint
（t为参数），C2：
x=8cosθ
y=3sinθ
（θ为参数）．
（1）化C1，C2的方程为普通方程，并说明它们分别表示什么曲线；
（2）若C1上的点P对应的参数为t=
π
2
，Q为C2上的动点，求PQ中点M到直线C3：
x=3+2t
y=-2+t
（t为参数）距离的最小值．                
C 已知函数f（x）=|x-a|．
（Ⅰ）若不等式f（x）≤3的解集为{x|-1≤x≤5}，求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，若f（x）+f（x+5）≥m对一切实数x恒成立，求实数m的取值范围．

已知命题p：?x∈[1，12]，x2-a≥0．命题q：?x0∈R，使得x数学公式+（a-1）x0+1＜0．
（1）若p或q为真，p且q为假，求实数a的取值范围．
（2）实数m分别取什么值时，复数z=m+1+（m-1）i是 ①实数？②虚数？③纯虚数？
(理)已知曲线C:f(x)=x2,C上点A、An的横坐标分别为1和an(n∈N*),且a1=5,xn+1=af(xn-1)+1(a＞0,a≠,a≠1).记区间Dn=［1,an］(an＞1).当x∈Dn时,曲线C上存在点Pn(xn,f(xn)),使得点Pn处的切线与直线AAn平行.

(1)试判断:数列{loga(xn-1)+1}是什么数列;

(2)当DnDn+1对一切n∈N*恒成立时,求实数a的取值范围;

(3)记数列{an}的前n项和为Sn,当a=时,试比较Sn与n+7的大小,并说明你的结论.

(文)已知f(x)=ax3+bx2+cx+d(a≠0)是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为(2,0),且f(x)在［-1,0］和［4,5］上有相同的单调性,在［0,2］和［4,5］上有相反的单调性.

(1)求c的值.

(2)在函数f(x)的图象上是否存在一点M(x0,y0),使得f(x)在点M处的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由.

(3)求|AC|的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网