题目内容
14.在△ABC中,若tanA>-1,则A的取值范围是(0,$\frac{π}{2}$)∪($\frac{3π}{4}$,π).分析 根据正切函数的图象与性质,结合三角形内角的取值范围,即可得出A的取值范围.
解答 解:△ABC中,A∈(0,π),
当tanA>-1时,π>A>$\frac{3π}{4}$,或$\frac{π}{2}$>A>0;
∴A的取值范围是(0,$\frac{π}{2}$)∪($\frac{3π}{4}$,π).
故答案为:(0,$\frac{π}{2}$)∪($\frac{3π}{4}$,π).
点评 本题考查了正切函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
19.若与球外切的圆台的上、下底面半径分别为r,R,则球的表面积为( )
| A. | 4π(r+R)2 | B. | 4πr2R2 | C. | 4πRr | D. | π(R+r)2 |
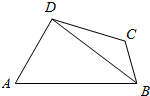 如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.