题目内容
1.定义[-1,1]上的奇函数f(x)是减函数,且f(1-a)+f(1-a2)>0,则实数a的取值范围是(1,$\sqrt{2}$].分析 根据题意,将题中不等式转化成f(1-a)<-f(1-a2),利用f(x)是定义在[-1,1]上的减函数得到关于a的不等式,解之即可得到实数a的取值范围.
解答 解:由f(1-a)+f(1-a2)>0,得f(1-a)>-f(1-a2).
∵f(x)是奇函数,
∴-f(1-a2)=f(a2-1).
于是f(1-a)>f(a2-1).
又由于f(x)在[-1,1]上是减函数,
因此$\left\{\begin{array}{l}{1-a<{a}^{2}-1}\\{-1≤1-a≤1}\\{-1≤{a}^{2}-1≤1}\end{array}\right.$,
解得1<a≤$\sqrt{2}$.
故答案为(1,$\sqrt{2}$].
点评 本题给出函数的单调性,求解关于a的不等式.着重考查了函数的奇偶性、单调性和不等式的解法等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列说法错误的是( )
| A. | 一个算法应包含有限的操作步骤,而不能是无限的 | |
| B. | 有的算法执行完后,可能有无数个结果 | |
| C. | 一个算法可以有0个或多个输入 | |
| D. | 算法中的每一步都是确定的,算法的含义是唯一的 |
11.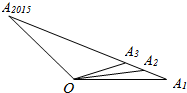 如图,O为直线A1A2015外一点,若A1,A2,A3,A4,A5…A2015中任意相邻两点的距离相等,设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$,其结果为( )
如图,O为直线A1A2015外一点,若A1,A2,A3,A4,A5…A2015中任意相邻两点的距离相等,设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$,其结果为( )
 如图,O为直线A1A2015外一点,若A1,A2,A3,A4,A5…A2015中任意相邻两点的距离相等,设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$,其结果为( )
如图,O为直线A1A2015外一点,若A1,A2,A3,A4,A5…A2015中任意相邻两点的距离相等,设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$,其结果为( )| A. | 2014($\overrightarrow{a}+\overrightarrow{b}$) | B. | 2015($\overrightarrow{a}+\overrightarrow{b}$) | C. | $\frac{2014}{2}$($\overrightarrow{a}+\overrightarrow{b}$) | D. | $\frac{2015}{2}$($\overrightarrow{a}+\overrightarrow{b}$) |
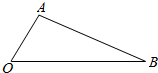 如图所示,在△AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,则△AOC为钝角三角形的概率为$\frac{2}{5}$.
如图所示,在△AOB中,已知∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,则△AOC为钝角三角形的概率为$\frac{2}{5}$.