题目内容
10.已知数列{an}是正项数列,且对于任意的n∈N*,an,Sn,an2都成等差数列.(1)求数列{an}的通项公式.
(2)设bn=an($\frac{1}{3}$)n,数列{bn}的前n项和是Tn,求Tn的值.
分析 (1)由an,Sn,an2成等差数列,且an>0可得2Sn=an+an2,令n=1,n≥2时,由an=Sn-Sn-1,进而可求公差,代入等差数列的通项公式可;
(2)运用数列的求和方法:错位相减法,结合等比数列的求和公式,化简即可得到.
解答 解:(1)∵an,Sn,an2成等差数列,且an>0,
∴2Sn=an+an2,①
当n=1时,有2a1=a1+a12∴a1=1,
当n≥2时,2Sn-1=an-1+an-12,②
①-②可得,2an=an-an-1+(an-an-1)(an+an-1),
化简得an-an-1=1,
∴数列{an}是1为首项,1为公差的等差数列,
则an=1+n-1=n;
(2)bn=an($\frac{1}{3}$)n=n•($\frac{1}{3}$)n,
Tn=1•$\frac{1}{3}$+2•($\frac{1}{3}$)2+3•($\frac{1}{3}$)3+…+n•($\frac{1}{3}$)n,
$\frac{1}{3}$Tn=1•($\frac{1}{3}$)2+2•($\frac{1}{3}$)3+3•($\frac{1}{3}$)4+…+n•($\frac{1}{3}$)n+1,
两式相减,可得$\frac{2}{3}$Tn=$\frac{1}{3}$+($\frac{1}{3}$)2+($\frac{1}{3}$)3+…+($\frac{1}{3}$)n-n•($\frac{1}{3}$)n+1
=$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$-n•($\frac{1}{3}$)n+1,
化简可得Tn=$\frac{3}{4}$-$\frac{3+2n}{4}$•$\frac{1}{{3}^{n}}$.
点评 本题主要考查了由数列的递推公式求解数列的通项,数列的求和方法:错位相减法,考查运算能力,属于中档题.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案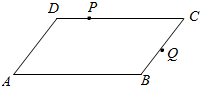 如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )
如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )| A. | $\frac{13}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{17}{2}$ | D. | $\frac{19}{2}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 800 | B. | 360 | C. | 240 | D. | 160 |