题目内容
(13分)如图,要在一块半径为1m,圆心为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M、N在
OB上,设∠BOP=θ.平行四边形MNPQ的面积为S.
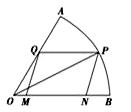
(1)求S关于θ的函数关系式;
(2)求S的最大值及相应θ的值.
OB上,设∠BOP=θ.平行四边形MNPQ的面积为S.

(1)求S关于θ的函数关系式;
(2)求S的最大值及相应θ的值.
解:(1)∠OQP中∠QOP=60°,∠OPQ=θ
由正弦定理:

过P作PE⊥OB于E, ∴ |PE|=|OP|sinθ=sinθ
∴ S=|PD|·|PQ|


(2)

当 时,S有最大值为
时,S有最大值为 。
。
由正弦定理:

过P作PE⊥OB于E, ∴ |PE|=|OP|sinθ=sinθ
∴ S=|PD|·|PQ|



(2)


当
 时,S有最大值为
时,S有最大值为 。
。略

练习册系列答案
相关题目
 在
在 上为增函数,其中
上为增函数,其中 ,
, 的取值集合;
的取值集合; ,若
,若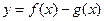 在
在

 =
= ,且
,且 .
.  ,试求
,试求 的值.
的值.
 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。 的最大值.
的最大值. 的取值范围,使不等式
的取值范围,使不等式 恒成立.
恒成立. 的终边上有一点
的终边上有一点 则
则 的值是( )
的值是( )




 的最小正周期;
的最小正周期;  ,求
,求 的值.
的值. 的图象的相邻两条对称轴的距离是
的图象的相邻两条对称轴的距离是 ,则
,则 的值为 .
的值为 .
