题目内容
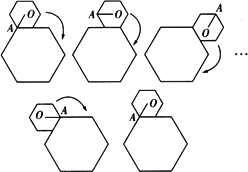
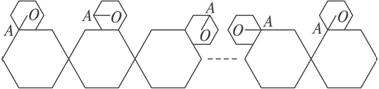
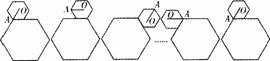
如下图,小正六边形沿着大正六边形的边,按顺时针方向滚动.小正六边形的边长是大正六边形边长的一半,如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中向量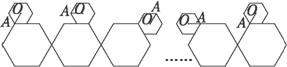
-1
解析:从第一图的开始位置变化到第二图时,向量![]() 围绕着点O旋转了-
围绕着点O旋转了-![]() 角(注意OA围绕着点O是顺时针旋转),从第二图的位置变化到第三图时,向量
角(注意OA围绕着点O是顺时针旋转),从第二图的位置变化到第三图时,向量![]() 围绕着点O旋转了-
围绕着点O旋转了-![]() ,则从第一图的开始位置变化到第三图的位置时,正好小正六边形滚过大正六边形的一条边,向量
,则从第一图的开始位置变化到第三图的位置时,正好小正六边形滚过大正六边形的一条边,向量![]() 围绕着点O旋转了-π角,则小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,向量
围绕着点O旋转了-π角,则小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,向量![]() 围绕着点O共旋转了-6π角,即θ=-6π,因而sin
围绕着点O共旋转了-6π角,即θ=-6π,因而sin![]() +cos
+cos![]() =sin(-π)+cos(-π)=-1.
=sin(-π)+cos(-π)=-1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
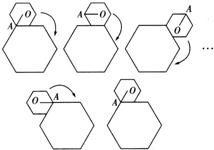 如图,小正六边形沿着大正六边形的边,按顺时针方向滚动.小正六边形的边长是大正六边形边长的一半,如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中向量
如图,小正六边形沿着大正六边形的边,按顺时针方向滚动.小正六边形的边长是大正六边形边长的一半,如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中向量