题目内容
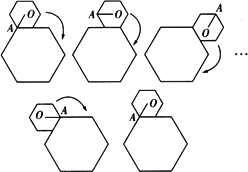
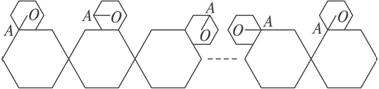
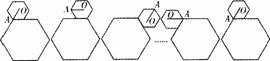
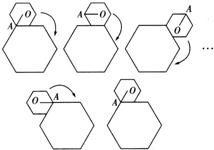 如图,小正六边形沿着大正六边形的边,按顺时针方向滚动.小正六边形的边长是大正六边形边长的一半,如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中向量
如图,小正六边形沿着大正六边形的边,按顺时针方向滚动.小正六边形的边长是大正六边形边长的一半,如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中向量| OA |
| θ |
| 12 |
| θ |
| 12 |
分析:小正六边形在大六边形边上转动时转动60°的角,在过大正六边形的角时转动120°,进而可求得小正六边形沿着大正六边形的边滚动一周后返回出发时的位置时,θ的值,代入原式即可.
解答:解:如图可知,向量
转了6个60°的角,6个120°
∴θ=-6×60°-6×120°=-1080°
∴sin
+cos
=sin(-90°)+cos(-90°)=-1
故答案为:-1
| OA |
∴θ=-6×60°-6×120°=-1080°
∴sin
| θ |
| 12 |
| θ |
| 12 |
故答案为:-1
点评:本题主要考查了三角函数的化简求值.考查了观察图形特点的能力,解题的关键是弄明白正六边形的中心角60°,内角为120°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目