题目内容
(2007
北京朝阳模拟)如下图，棱长为1的正四面体ABCD中，E、F分别是棱AD、CD的中点，D是点A在平面BCD内的射影．(1)
求直线EF与直线BC所成角的大小；(2)
求点O到平面ACD的距离；(3)
求二面角A－BE－F的大小．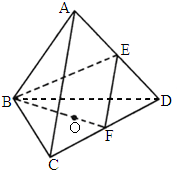
答案：略
解析：
解析：
|
解析： (1)因为E、F分别是棱AD、CD的中点．所以EF∥AC．所以∠ BCA是EF与BC所成角．∵正四面体 ABCD，∴△ABC为正三角形，所以∠ BCA=60°．即 EF与BC所成角的大小是60°．(2) 如图，连结AO，AF，因为F是CD的中点，且△ACD，△BCD均为正三角形，所以 BF⊥CD，AF⊥CD．因为  ，所以CD⊥面AFB．
因为  面ACD．所以面AFB⊥面ACD．
因为 ABCD是正四面体，且O是点A在面BCD内的射影，所以点O必在正三角形BCD的中线BF上．在面 ABF中，过O做OG⊥AF，垂足为G．所以OG⊥面ACD．即 OG的长为点O到面ACD的距离．因为正四面体 ABCD的棱长为1，在△ ABF中，容易求出 ，
因为△ AOF∽△OGF，故由相似比易求出 ．
所以点 O到平面ACD的距离是 ．
(3) 设△ABD中，AB边的中线交BE于H，连结CH，则由ABCD为正四面体知CH⊥面ABD．设 HD的中点为K，则FK∥CH．所以FK⊥面ABD．在面 ABD内，过点K作KN∥AD，KN交BE于M，交AB于N，因为 BE⊥AD，所以NM⊥BE．连结 FM，所以FM⊥BE．所以∠ NMF是所求二面角的平面角．
因为  ，
所以  ．
所以  ．
所以所求二面角的大小为 
( 或者由正四面体的对称性，可转求二面角 的大小)． |
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
(a≠0)是定义在R上的函数，其图象交x轴于A、B、C三点．若点B的坐标为(2，0)，且f(x)在[－1，0]和[4，5]上有相同的单调性，在[0，2]和[4，5]上有相反的单调性．
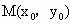使得f(x)在点M处的切线斜率为3b?若存在，求出点M的坐标；若不存在，请说明理由；
(m＞1)，
．
在轨迹W上，直线PF交轨迹W于点Q，且
，若1≤λ≤2，求实数m的范围．
，
，动点M到定直线y=1的距离等于d，并且满足
，其中O为坐标原点，k为参数．
，求实数k的取值范围．
且不等式
的解集是(－∞，－2]∪[0，2]，则实数a的值是_________．