题目内容
8.若关于x的不等式|x-1|-|x+m|≥a有解时,实数a的最大值为5,则实数m的值为4或-6.分析 令f(x)=|x-1|-|x+m|,运用绝对值不等式的性质可得f(x)的最大值|m+1|,由题意可得|m+1|=5,解得m即可.
解答 解:令f(x)=|x-1|-|x+m|,
由|x-1|-|x+m|≤|(x-1)-(x+m)|=|m+1|,
可得f(x)的最大值为|m+1|,
关于x的不等式|x-1|-|x+m|≥a有解,
即为a≤|m+1|,
又实数a的最大值为5,
则|m+1|=5,
解得m=4或-6.
故答案为:4或-6.
点评 本题考查绝对值不等式的性质,主要考查不等式成立问题转化为求函数最值问题,属于基础题和易错题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
3.执行如图所示的程序框图,则输出S的值是( )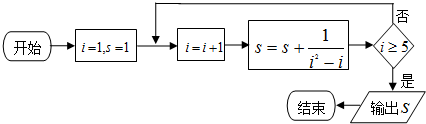

| A. | $\frac{4}{5}$ | B. | $\frac{9}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{11}{6}$ |
17.执行如图的程序框图,若输入的x为6,则输出的y的值为( )


| A. | 6 | B. | 4 | C. | 3 | D. | 2.5 |
16.若复数$\frac{a+3i}{1+2i}$(α∈R,i为虚数单位)是纯虚数,则实数α的值为( )
| A. | -6 | B. | -4 | C. | 4 | D. | 6 |