题目内容
13.设函数y=f(x)由方程$\frac{x•|x|}{16}$-$\frac{y•|y|}{9}$=1确定,下列结论正确的是(1)(2)(4).(请将你认为正确的序号都填上)(1)f(x)是R上的单调递增函数;
(2)不等式f(x)=$\frac{3}{4}$x<0的解集为R;
(3)方程f(x)+$\frac{3}{4}$x-3=0恒有两解;
(4)f(x)存在反函数f-1(x),且反函数f-1(x)由方程$\frac{y•|y|}{16}$-$\frac{x•|x|}{9}$=1确定.
分析 由方程$\frac{x•|x|}{16}$-$\frac{y•|y|}{9}$=1,对x,y分类讨论,画出其图象,利用椭圆与双曲线的性质即可判断出.
解答 解:方程$\frac{x•|x|}{16}$-$\frac{y•|y|}{9}$=1,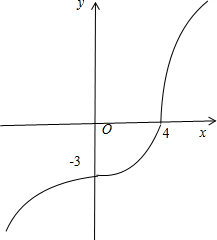
当x≥0,y≥0时,化为$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}=1$;当x≥0,y<0时,化为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1;
当x<0,y>0时,化为-$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1;当x<0,y<0时,化为-$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1.画出图象.
由图象可知:(1)正确;
(2)∵$y=\frac{3}{4}x$为双曲线$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}=1$;及-$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的渐近线,因此不等式f(x)-$\frac{3}{4}$x<0的解集为R,正确;
(3)方程f(x)+$\frac{3}{4}$x-3=0恒有一解,因此不正确;
(4)由(1)可知f(x)是R上的单调递增函数,因此f(x)存在反函数f-1(x),且反函数f-1(x)由方程$\frac{y•|y|}{16}$-$\frac{x•|x|}{9}$=1确定,正确.
故答案为:(1)(2)(4).
点评 本题考查了椭圆与双曲线标准方程图象及其性质,考查了分类讨论思想方法、数形结合思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知三棱锥P-ABC的四个顶点均在同一球面上,其中△ABC为等边三角形,PA⊥平面ABC,PA=2AB=2a,则该球的体积是( )
| A. | $\frac{\sqrt{2}}{27}$πa2 | B. | $\frac{32\sqrt{2}}{27}$πa2 | C. | $\frac{32\sqrt{3}}{27}$πa3 | D. | $\frac{32\sqrt{3}}{9}$πa3 |
1.已知集合A={x|$\frac{1}{x}$<1},B={y|y=2-x-1,x∈R},则A∩B=( )
| A. | ∅ | B. | {x|x>1} | C. | {x|-1<x<0} | D. | {x|-1<x<0或x>1} |
18.已知函数g(x)=$\left\{\begin{array}{l}{\frac{1}{x+1}-3,-1<x≤0}\\{{x}^{2}-3x+2,0<x≤1}\end{array}\right.$,若方程g(x)-mx-m=0有且仅有两个不等的实根,则实数m的取值范围是( )
| A. | (-$\frac{9}{4}$,-2]∪[0,2] | B. | (-$\frac{11}{4}$,-2]∪[0,2] | C. | (-$\frac{9}{4}$,-2]∪[0,2) | D. | (-$\frac{11}{4}$,-2]∪[0,2) |
1.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x},}&{x≤0}\\{lo{g}_{2}}&{x,x>0}\end{array}\right.$,若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
1.已知某班学生语文与数学的学业水平测试成绩抽样统计如下表,若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示语文成绩与数学成绩,例如:表中语文成绩为B等级的共有20+18+4=42人,已知x与y均为B等级的概率是0.18.
(Ⅰ)求抽取的学生人数;
(Ⅱ)设该样本中,语文成绩优秀率是30%,求a,b的值;
(Ⅲ)已知a≥10,b≥8,求语文成绩为A等级的总人数比语文成绩为C等级的总人数少的概率.
| x语文 人数 y数学 | A | B | C |
| A | 7 | 20 | 5 |
| B | 9 | 18 | 6 |
| C | a | 4 | b |
(Ⅱ)设该样本中,语文成绩优秀率是30%,求a,b的值;
(Ⅲ)已知a≥10,b≥8,求语文成绩为A等级的总人数比语文成绩为C等级的总人数少的概率.