题目内容
将进货单价为80元的商品按90元一个售出时,能卖出400个,已知该商品每个涨价1元,其销售量就减少20个,为了赚得最大利润,售价应定为( )
| A.每个95元 | B.每个100元 | C.每个105元 | D.每个110元 |
A.
解析试题分析:利润=(销售价格-进价) 销售量,可设售价为x元,利润为y元.由题意可得:
销售量,可设售价为x元,利润为y元.由题意可得: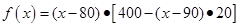
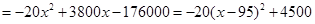
由二次函数的图像知,当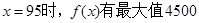 .
.
考点:应用问题转化为数学问题 .

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设f(x)=lgx+x-3,用二分法求方程lgx+x-3=0在(2,3)内近似解的过程中得f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,则方程的根落在区间( )
| A.(2,2.25) | B.(2.25,2.5) |
| C.(2.5,2.75) | D.(2.75,3) |
函数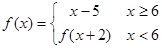 ,则
,则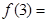 ( )
( )
| A.5 | B.4 | C.3 | D.2 |
函数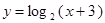 的反函数是( )
的反函数是( )
A. | B. |
C. | D. |
已知数列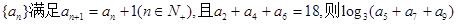 等于( )
等于( )
| A.2 | B.—2 | C.—3 | D.3 |
设函数 是R上的单调递减函数,则实数a的取值范围为( )
是R上的单调递减函数,则实数a的取值范围为( )
| A.(-∞,2) | B.(-∞, ] ] | C.(0,2) | D.[ ,2) ,2) |
若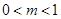 ,则( )
,则( )
A. | B.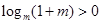 |
C.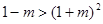 | D.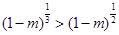 |
已知函数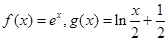 ,对任意
,对任意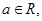 存在
存在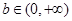 使
使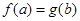 ,则
,则 的最小值为( )
的最小值为( )
A.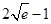 | B.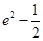 | C.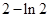 | D.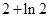 |
若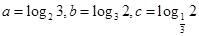 ,则
,则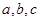 的大小关系是( )
的大小关系是( )
A.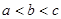 | B. | C.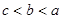 | D.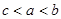 |