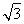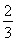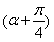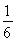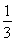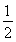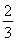题目内容
(13分)已知圆O:x2+y2=3的半径等于椭圆E: =1(a>b>0)的短半轴长,椭圆E的右焦点F在圆O内,且到直线l:y=x-
=1(a>b>0)的短半轴长,椭圆E的右焦点F在圆O内,且到直线l:y=x- 的距离为
的距离为 -
- ,点M是直线l与圆O的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆O的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).

(1)求椭圆E的方程;
(2)求证:|AF|-|BF|=|BM|-|AM|.
(1)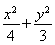 =1(2)见解析
=1(2)见解析
【解析】(1)设点F(c,0)(c>0),则F到直线l的距离为 =
=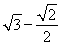 ,即|c-
,即|c-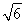 |=
|=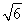 -1,
-1,
因为F在圆O内,所以c<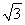 ,故c=1.
,故c=1.
又因为圆O的半径等于椭圆E的短半轴长,所以b2=3,
所以所求椭圆方程为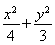 =1.
=1.
(2)证明:因为圆心O到直线l的距离为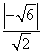 =
=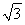 ,所以直线l与圆O相切,M是切点,故△AOM为直角三角形,所以|AM|=
,所以直线l与圆O相切,M是切点,故△AOM为直角三角形,所以|AM|=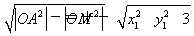 ,又
,又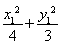 =1,可得|AM|=
=1,可得|AM|=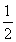 x1,
x1,
|AF|=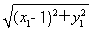 ,又
,又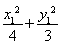 =1,可得|AF|=2-
=1,可得|AF|=2-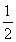 x1,
x1,
所以|AF|+|AM|=2,同理可得|BF|+|BM|=2,
所以|AF|+|AM|=|BF|+|BM|,即|AF|-|BF|=|BM|-|AM|.

练习册系列答案
相关题目